Задача 1. Предприниматель купил 3 торговых зоны (А, В, С) в сельской зоне

Предприниматель купил 3 торговых зоны (А, В, С) в сельской зоне. Ему нужно выбрать место для склада Х, до которого нужно отремонтировать дороги. Где выбрать Х так, чтобы минимизировать затраты на ремонт дорог и перевозку товаров. Считаем, что затраты на ремонт пропорциональны + + 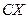, а затраты на перевозку пропорциональны 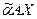+ + ( — площади торговых зон).

Для решения задач я буду использовать хорошо известный принцип упорядоченных наборов для трёх чисел: если 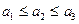, , 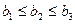то , где — некоторая перестановка . Его доказательство представлено в [6, стр. 14].

Решение

Возможны такие случаи:

1. Все углы АВС меньше 120˚.

2. Треугольник АВС имеет больший угол равный или больший 120˚.

3. Точки А, В, С лежат на одной прямой.

Для первого случая ответом является точка Торричелли. По её свойству:

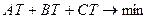, значит .

Для второго случая ответом будет точка Ферма, которая будет совпадать с вершиной тупого угла.

Если точки А, В, С образуют прямую, то совпадает с точкой, лежащей между двумя другими.

Пусть 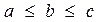и 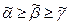. По доказанному неравенству:

.

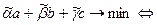
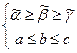В отличие от стандартной задачи Ферма – Торричелли – Штейнера здесь введены коэффициенты при длинах расстояний и способ решения этой задачи. Используя теорему о принадлежности точки Торричелли зонам Дирихле вершин треугольника и зная длины 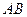, , можно упорядочить расстояния , , 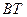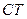наибольшее и наименьшее.

Дата добавления: 2015-07-25