
Читайте также:
|
Точка Р, лежащая внутри  , называется первой точкой Брокара (рис. 1.8), если
, называется первой точкой Брокара (рис. 1.8), если  . Точка Q, лежащая внутри
. Точка Q, лежащая внутри  , называется второй точкой Брокара (рис. 1.9), если
, называется второй точкой Брокара (рис. 1.9), если  .
.
Известно, что  ([4, стр. 23]). Угол
([4, стр. 23]). Угол  называют углом Брокара.
называют углом Брокара.
1.5.1. При каких условиях первая (вторая) точка Брокара
находится на пересечении зон Дирихле всех вершин треугольника?
Это возможно только в том случае, если точка Р (Q) совпадает с центром описанной окружности. Пусть это так (рис. 1.10). Имеем 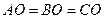 , так как
, так как  — центр описанной окружности
— центр описанной окружности 
 ,
,  ,
,  — равнобедренные
— равнобедренные 

 ,
,  ,
,  (как углы при основании равнобедренных треугольников). Так как
(как углы при основании равнобедренных треугольников). Так как 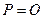 – первая точка Брокара, то
– первая точка Брокара, то 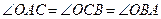

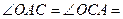

 , то есть
, то есть  (
( — равносторонний). Аналогично, вторая точка Брокара (Q) совпадает с центром описанной окружности только в правильном треугольнике.
— равносторонний). Аналогично, вторая точка Брокара (Q) совпадает с центром описанной окружности только в правильном треугольнике.
1.5.2. При каких условиях первая точка Брокара
принадлежит зоне Дирихле вершины А?
Задание: найти условия на элементы треугольника, при которых верно:
 .
.
А) Из  имеем:
имеем: 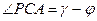 ,
,  ,
,
 или
или 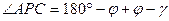 , то есть
, то есть  .
.
Б) Из 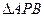 имеем:
имеем:  ,
,  ,
,
 или
или 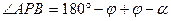 , то есть
, то есть  .
.
В) Из  имеем:
имеем:  ,
,  ,
,
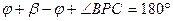 или
или  , то есть
, то есть  .
.
По теореме синусов (для  ,
, 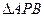 ,
,  ):
):
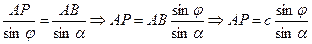
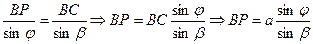
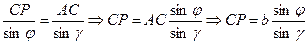
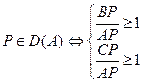
Решим предыдущую систему. Начнём с первого неравенства.
 .
.
По теореме синусов: 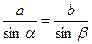 ,
, 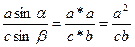 .
.
Значит, 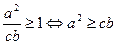 .
.
Рассмотрим второе неравенство. 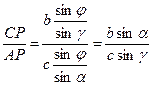 .
.
По теореме синусов:  ,
, 
Значит,  .
.
Система  верна при
верна при 
Вывод: 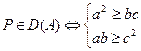 .
.
1.5.3. При каких условиях вторая точка Брокара
принадлежит зоне Дирихле точки А?
Задание: найти условия элементов треугольника, при которых верно:
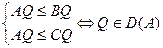 .
.
А) Из  имеем:
имеем:  ,
, 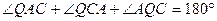 ,
,
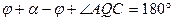 или
или  , то есть
, то есть 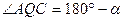 .
.
Б) Из  имеем:
имеем:  ,
, 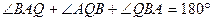 ,
,
 или
или  , то есть
, то есть 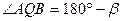 .
.
В) Из  имеем:
имеем: 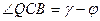 ,
,  ,
,
 или
или 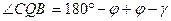 , то есть
, то есть  .
.
По теореме синусов:
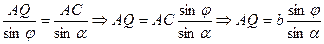 .
.
 .
.
 .
.
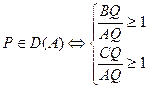 .
.
Решим предыдущую систему. Начнём с первого неравенства.

По теореме синусов: 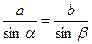 ,
, 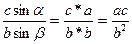 .
.
Значит,  .
.
Рассмотрим второе неравенство.  .
.
По теореме синусов:  ,
, 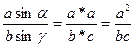 .
.
Значит, 
Система 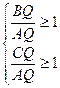 верна при
верна при 
Вывод: 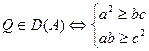 .
.
При каких условиях обе точки Брокара
принадлежат зоне Дирихле вершины А?
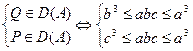 .
.
Дата добавления: 2015-07-25; просмотров: 137 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Инцентр | | | Точка Торричелли |