Задача 5. Доказать: 1) L – центроид ; 2)

Дано: , , 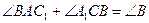, , 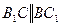, , 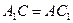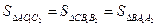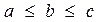(см. рис. 2.4).

Доказать: 1) L – центроид ; 2) .

В решении использована следующая интересная вспомогательная лемма, которая вытекает из теоремы Чевы (см. приложение «Интересный факт», рис. 2.5).

Решение

1. Проведём , .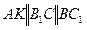

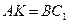2. 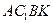— параллелограмм (, ).

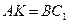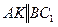Следовательно, .

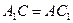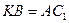3. Так как и , то 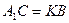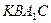— параллелограмм (, ).

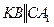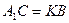4. Так как , то — вершина параллелограмма (по доказанной лемме из приложений к работе — с. 32, рис. 2.5).

5. Так как , , 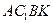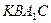- параллелограммы, то по свойству диагоналей параллелограмма:

,

,

.

6. Так как 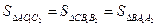, то = = 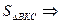К – центроид

L=K L – центроид , что и требовалось доказать.

7. Так как , то по теореме о принадлежности центроида зонам Дирихле вершин треугольника 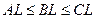, ч. т. д.

ВЫВОДЫ

В работе проведены исследования и выяснены условия принадлежности основных замечательных точек треугольника зонам Дирихле вершин треугольника в «евклидовой» метрике. Рассматриваются такие точки, как ортоцентр (Н), инцентр (I), центроид (М), центр описанной окружности (O), 2 точки Брокара (P та Q), точка Торричелли (Т). Доказано, что точка О лежит на пересечении зон Дирихле всех вершин треугольника, точки Н, I, М, Т принадлежат зоне Дирихле вершины большего угла треугольника, для точек P и Q определены специфические условия их принадлежности сферам влияния вершин треугольника. Полученные результаты сформулировано в виде теоремы. Также составлено и решено 5 авторских задач, в которых используется эта теорема. Параллельно были изучены понятия метрика, расстояние, метрическое пространство и зоны Дирихле в метрических пространствах, рассмотрены способы деления пространства на зоны Дирихле, практическое применение зон Дирихле. Также были написаны три программы по теме работы на Delphi 7 для персонального компьютера, которые автоматизируют деление плоскости на зоны Дирихле, а также определение принадлежности точек сферам влияния в разных метриках.

Все основные результаты работы получено самостоятельно. Они не содержатся в доступной автору литературе по теме.

Дата добавления: 2015-07-25