Ортоцентр

Высота треугольника — прямая СD (рис. 1.1) опущенная из вершины треугольника перпендикулярно к прямой, содержащей противоположную сторону. Ортоцентр – точка пересечения высот в треугольнике. Ортоцентр лежит внутри треугольника в случае остроугольного треугольника, на вершине прямого угла в прямоугольном треугольнике, и вне треугольника – в тупоугольном.

1.2.1. При каких условиях ортоцентр

находится на пересечении зон Дирихле?

Высоты треугольника пересекаются в одной точке, называемой ортоцентром. Он совпадает с центром описанной окружности тогда и только тогда, когда 3 высоты совпадают с тремя серединными перпендикулярами. Если это будет верно для 3 сторон, то получим равносторонний треугольник (рис. 1.2).

Точка О (ортоцентр и центр описанной окружности) находится на пересечении зон Дирихле. В этом случае углы треугольника АВС равны.

1.2.2. При каких условиях ортоцентр принадлежит

зоне Дирихле вершины А?

Так как в зависимости от мер углов треугольника ортоцентр может лежать как внутри треугольника, так и совпадать с его вершиной, так и быть вне треугольника, то рассмотрим отдельно случаи остроугольного, прямоугольного и тупоугольного треугольника.

1.2.2.1. Для остроугольного треугольника:

Гипотеза: , то есть .

Пусть угол А – больший (рис. 1.3.). Имеем: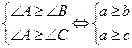

Из 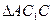и имеем , .

Докажем, что 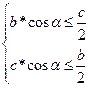или при

Из теоремы косинусов имеем: .

Докажем требуемые неравенства.

А) 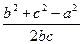умножим на , ,

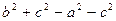
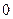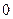, , так как , то , ч. т. д.

Б) 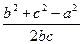умножим на , ,

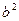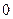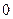, , так как , то , ч. т. д.

Значит, система верна при .

Вывод: , ч. т. д.

1.2.2.2. Для прямоугольного треугольника:

Так как ортоцентр всегда лежит в вершине прямого угла, то он принадлежит его зоне Дирихле.

Вывод: .

1.2.2.3. Для тупоугольного треугольника:

В тупоугольном треугольнике ортоцентр лежит на продолжении высоты проведенной из вершины тупого угла (рис 1.4). Так как в любом треугольнике против большего угла лежит большая сторона и тупой угол больше острого, то:

А) Из имеем .

Б) Из имеем .

Значит, в тупоугольном треугольнике 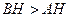и .

Вывод: .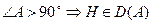

Дата добавления: 2015-07-25