Читайте также:
|
Теорема. (О принадлежности замечательных точек треугольника зоне Дирихле его вершины). Центр описанной окружности всегда находится на пересечении зон Дирихле вершин треугольника. Ортоцентр, инцентр, центроид, точка Торричелли принадлежат зоне Дирихле вершины большего угла. Точки Брокара принадлежат зоне Дирихле вершины А, если выполняются соотношения:
, 
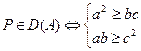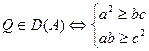или 
.
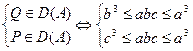Следствие (О принадлежности замечательных точек треугольника пересечению зон Дирихле его вершин).
Условия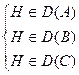 
, 
, 
, 
, 
, 
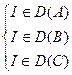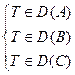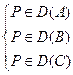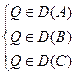верны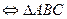 
— правильный.
Дата добавления: 2015-07-25; просмотров: 63 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Точка Торричелли | | | Задача 1. |