Инцентр

Биссектриса – луч, делящий угол пополам. Инцентр — точка пересечения биссектрис треугольника. Также инцентр является центром вписанной в треугольник окружности. Инцентр всегда лежит внутри треугольника.

1.4.1. При каких условиях инцентр

находится на пересечении зон Дирихле всех вершин треугольника?

Найдём условия на элементы треугольника, при которых инцентр совпадает с центром описанной окружности. Пусть они совпадают (рис 1.6).

Имеем 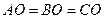, так как — центр описанной окружности , , — равнобедренные , , (как углы при основании равнобедренных треугольников). Так как , , — биссектрисы , то 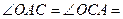, то есть ( — равносторонний).

Инцентр лежит на пересечении зон Дирихле всех вершин треугольника в равностороннем треугольнике.

1.4.2. При каких условиях инцентр

принадлежит зоне влияния точки А?

Гипотеза: .

Доказательство

Точками касания окружность делит стороны треугольника на 6 частей (рис. 1.7), для которых выполняется система:

(1.1)

Пусть , тогда .

Тогда , то есть проекции отрезка на , меньше, чем и соответственно. Преобразуем систему (1.1): , , .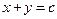

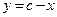Далее , , , ,

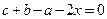или .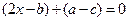

Так как то:

и .

Значит, .

Вывод: .

Дата добавления: 2015-07-25