Список условных обозначений

СОДЕРЖАНИЕ

СОДЕРЖАНИЕ.. 2

СПИСОК УСЛОВНЫХ ОБОЗНАЧЕНИЙ.. 3

ВВЕДЕНИЕ.. 4

РАЗДЕЛ 1. О ПРИНАДЛЕЖНОСТИ НЕКОТОРЫХ ЗАМЕЧАТЕЛЬНЫХ ТОЧЕК ТРЕУГОЛЬНИКА ЗОНАМ ДИРИХЛЕ ЕГО ВЕРШИН.. 6

· 1.1. Центр описанной окружности. 6

· 1.2. Ортоцентр. 6

· 1.3. Центроид. 8

· 1.4. Инцентр. 10

· 1.5. Точки Брокара. 11

· 1.6. Точка Торричелли. 15

· 1.7. Теорема о принадлежности замечательных точек треугольника зонам Дирихле его вершин 16

РАЗДЕЛ 2. ЗАДАЧИ.. 17

· 2.1. Задача 1. 17

· 2.2. Задача 2. 18

· 2.3. Задача 3. 18

· 2.4. Задача 4. 19

· 2.5. Задача 5. 20

ВЫВОДЫ... 22

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ.. 23

ПРИЛОЖЕНИЯ.. 24

1. Рисунки к основной части работы.. 24

2. Метрические пространства и зоны Дирихле. 27

· Какие бывают расстояния. 27

· Шары.. 28

· Аксиомы метрики. 29

· Зоны Дирихле в метрических пространствах и их приложения. 30

3. Интересный факт. 32

4. Компьютерное приложение к работе. 34

СПИСОК УСЛОВНЫХ ОБОЗНАЧЕНИЙ

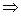Знак логического следования.

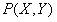Расстояние между точками X, Y.

А 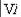В «Сравним величины А и В».

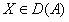Точка Х принадлежит зоне Дирихле точки А.

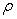Название евклидовой метрики, заданной формулой

() .

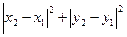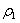Название городской метрики, заданной формулой

.

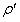Название метрики, заданной формулой

().

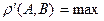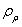Название метрики, заданной формулой

()

Дата добавления: 2015-07-25