Читайте также:
|
Даны 3 точки плоскости (А, В, С), образующие треугольник АВС, известны длины его сторон. Найти точку Х внутри треугольника такую, что 
(рис 2.1). Пусть даны 
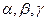— некоторые положительные числа. Каким образом нужно расставить коэффициенты 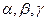таким образом, чтобы минимизировать величину 
, где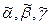 
— некоторые перестановки 
.
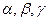Решение
1. Умножим 
на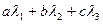 
. Имеем:
= 
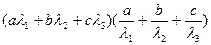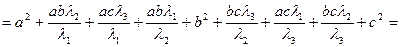
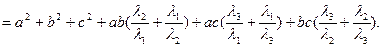
По неравенству Коши (неравенство о среднем арифметическом и среднем геометрическом): 
, 
, 
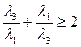, значит:
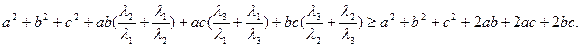
Равенство достигается при
, 
, 
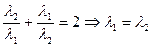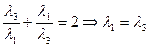или 
, т. е. Х=I (инцентр).
Если даны коэффициенты 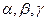, то решение задачи 
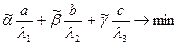аналогично решению второй части задачи №1.
Дата добавления: 2015-07-25; просмотров: 66 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Задача 2. | | | Задача 4. |