Читайте также:
|
Точка Торричелли — точка треугольника (рис. 1.11), из которой все стороны видны под углом в 120°. Существует только в треугольниках с углами меньшими 120° [5].
1.6.1. При каких условиях точка Торричелли
находится на пересечении зон влияния?
Точка находится на пересечении зон Дирихле, если 
, а так как 
, значит 
, следовательно, 
является равносторонним.
1.6.2.При каких условиях точка Торричелли
принадлежит зоне Дирихле вершины А?
Задание: найти условия на элементы треугольника, при которых выполняется система:
(1.2).
По теореме косинусов:
, 
, значит
Пусть система (1.2) верна, тогда:
.
.
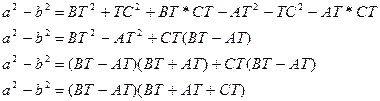
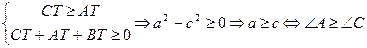Значит система (1.2) выполняется при 
.
Вывод: 
.
Дата добавления: 2015-07-25; просмотров: 67 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Точки Брокара | | | Теорема о принадлежности замечательных точек треугольника зонам Дирихле его вершин |