Читайте также:
|
Любой вектор векторного пространства можно разложить по его базису и притом единственным способом. т.е. координаты вектора относительно базиса определяются однозначно
Теперь докажем единственность разложения по базису. Допустим противное. Пусть имеется два разложения вектора 
по базису 
векторного пространства 
: 
и 
. Получаем равенство
, откуда следует 
. Если 
, то 
, а т.к. 
, то 
и коэффициенты разложения равны: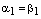 
, 
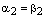. Пусть теперь 
. Тогда 
, где 
. По теореме о коллинеарности двух векторов отсюда следует, что 
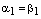. Получили противоречие условию теоремы. Следовательно, и 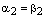, ч.т.д.
Дата добавления: 2015-07-25; просмотров: 84 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Линейная зависимость и независимость системы векторов. Пусть имеется n векторов. | | | Подпространство |