Читайте также:
|
2. Нера́венство Коши́ — Буняко́вского связывает норму и скалярное произведение векторов в линейном пространстве. Это неравенство эквивалентно неравенству треугольника для нормы в пространстве со скалярным произведением.
Пусть дано линейное пространство 
со скалярным произведением 
. Пусть 
- норма, порождённая скалярным произведением, то есть 
. Тогда для любых 
имеем
.
3. Если оба вектора ненулевые, то косинус угла между ними вычисляется по формуле:
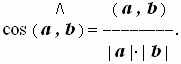
Дата добавления: 2015-07-25; просмотров: 58 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Метод Гаусса. | | | Линейная зависимость и независимость системы векторов. Пусть имеется n векторов. |