Читайте также:
|
Составим линейную комбинацию:
, если 
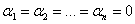
система n векторов – линейно-зависима.
Если среди n векторов какие-то k линейно-зависимы, то вся система векторов
является линейно-зависимой.
Если система n векторов линейно-независима, то любая часть из этих векторов
будет тоже линейно-независимой.
41. Система векторов линейного пространства L образует базис в L если эта система векторов упорядочена, линейно независима и любой вектор из L линейно выражается через векторы системы.
Иными словами, линейно независимая упорядоченная система векторов e 1,..., e n
образует базис в L если любой вектор x из L может быть представлен в виде
x = С1· e 1+С2 ·e 2+...+С n · e n.
Пример: Система векторов · i, j + k, i − j − k линейного пространства R3 геометрических радиусов векторов трехиерного пространства линейно зависима.
Вектор i − j − k линейно выражается через векторы i и j + k: i − j − k = i − (j + k).
Дата добавления: 2015-07-25; просмотров: 42 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Скалярным произведением двух векторов называется число, равное произведению модулей этих векторов на косинус угла между ними | | | Теорема. (О разложении вектора по базису.) |