
Читайте также:
|
Для того чтобы система линейных уравнений AX = B была совместной, необходимо и достаточно, чтобы ранг её матрицы был равен рангу расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных. Система совместна, если rangA = rangD. Очевидно, что система (1) может быть записана в виде:
x1  + x2
+ x2  + … + xn
+ … + xn 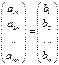
Доказательство.1) Если решение существует, то столбец свободных членов есть линейная комбинация столбцов матрицы А, а значит добавление этого столбца в матрицу, т.е. переход А®А* не изменяют ранга.2) Если RgA = RgA*, то это означает, что они имеют один и тот же базисный минор. Столбец свободных членов – линейная комбинация столбцов базисного минора, те верна запись, приведенная выше.
Дата добавления: 2015-07-25; просмотров: 77 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Формулы Крамера. | | | Метод Гаусса. |