
Читайте также:
|
Пусть  - непрерывно дифференцируемая функция в точке
- непрерывно дифференцируемая функция в точке  . Если
. Если  - точка локального минимума (максимума) функции
- точка локального минимума (максимума) функции  , то
, то
 (2)
(2)
Доказательство
 (3)
(3)


 (4)
(4)
Представим 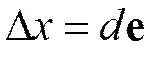 ,
, 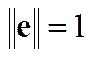
где  ,
,  – единичный вектор, совпадающий по направлению с вектором
– единичный вектор, совпадающий по направлению с вектором  ,
,  .
.
Тогда (4)
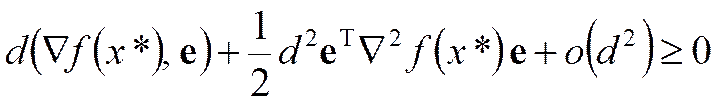
или
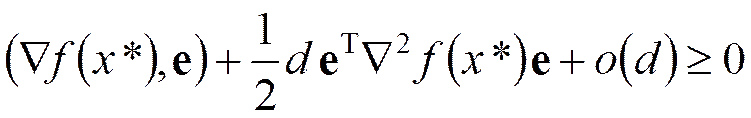 (5)
(5)

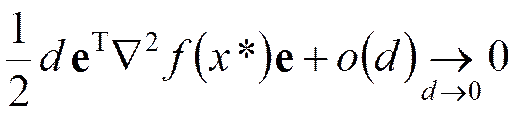
 (6)
(6)

 (7)
(7)
Точки  , удовлетворяющие условию (2), называются стационарными точками функции
, удовлетворяющие условию (2), называются стационарными точками функции  или задачи (1).
или задачи (1).
Для выявления искомой точки на множестве стационарных используется условие локальной оптимальности второго рода
Дата добавления: 2015-07-25; просмотров: 52 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Постановка и схема решения задачи | | | Теорема 2 |