Читайте также:
|
Задача безусловной оптимизации
Постановка и схема решения задачи
Данные: 
;
Модель: 
;
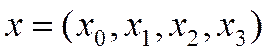- управляющие переменные;
Задача безусловной оптимизации имеет вид:
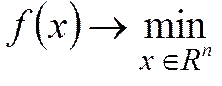(1)
Предполагается, что функция 
дважды непрерывно дифференцируема всюду на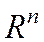 
, т.е. в точке 
имеет градиент
и матрицу Гессе
.
Схема решения задачи оптимизации может выглядеть следующим образом:
1. Находятся все точки локальных минимумов (максимумов);
2. Вычисляются значения функции 
во всех найденных точках локальных минимумов (максимумов) и выбирается точка (точки) с наименьшим (наибольшим) значением функции. Она и составит решение задачи.
Дата добавления: 2015-07-25; просмотров: 58 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| проведения Дней городов и районов в муниципальных образованиях Тверской области в 2015 г. | | | Теорема 1 Необходимое условие наличия локального экстремума |