|
Читайте также: |
Теорема Вейерштрасса. Пусть в задаче условной оптимизации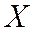 
- компакт в 
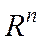, целевая функция 
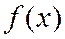непрерывна на 
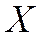. Тогда существует точка глобального минимума (максимума) функции 
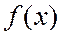на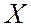 
.
Замечание 1. Множество Х называется замкнутым, если оно содержит все свои внутренние и граничные.
Дата добавления: 2015-07-25; просмотров: 78 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Замечание 2 | | | Замечание 3.Ограниченное замкнутое множество Х называется компактным (компактом). |