Методы сопряженных направлений

а) - квадратичная ЦФ

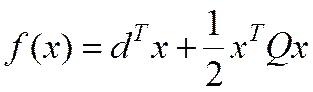(12)

Определение. Пусть 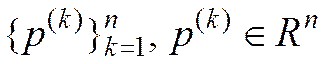- система 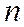линейно независимых векторов, 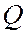- симметрическая неотрицательно определенная матрица; при этом выполняются условия

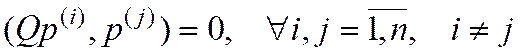(13)

Тогда совокупность векторов называется системой сопряженных направлений относительно матрицы .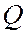

Определение. Алгоритм

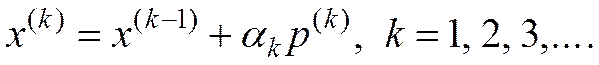, (14)

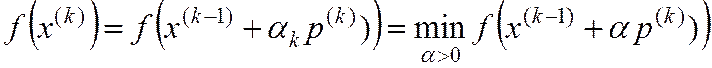(15)

при (13) называется методом сопряженных направлений

Утверждение

- система сопряженных направлений относительно матрицы .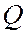

Тогда (14) в случае (12) при условии (15) и произвольном 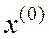за 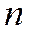шагов обеспечивает достижение точки минимума (12), т.е.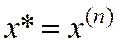

Формирование системы сопряженных направлений

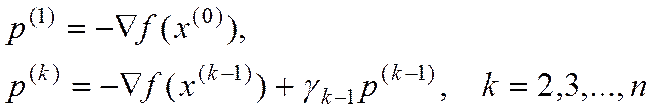(16)

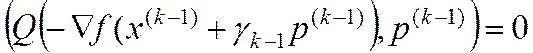
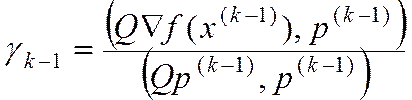(17)

б) ЦФ не является квадратичной

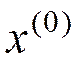
1. 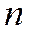вычислений (14),(15) при (16)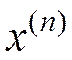, (18) ;

(18)

2. Проверка выполнения условий останова:

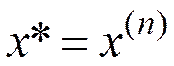
Условия выполняются Поиск завершен;

Условия не выполняются

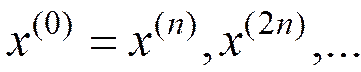
Идти к п.1

Метод сопряженных градиентов (метод Ривса), метод первого порядка

в) Лемма.

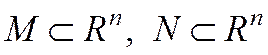- подпространства;

;

-

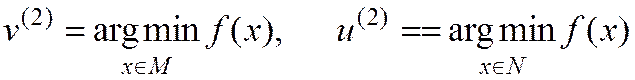точки минимума функции в подпространствах

при поиске вдоль направления .

Тогда вектор 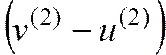сопряжен с направлением

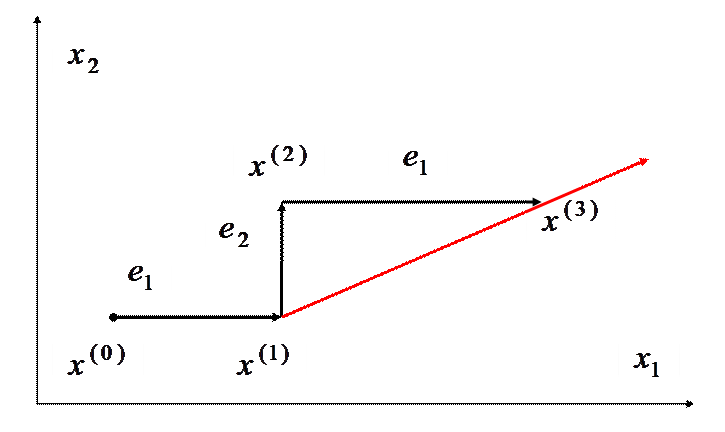
Рис. 1

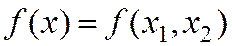
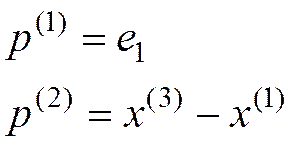
Дата добавления: 2015-07-25