Замечание 3.Ограниченное замкнутое множество Х называется компактным (компактом).

Определение 1. Численный метод - это правило (алгоритм), в соответствии с которым вычисляется последовательность точек , которая должна сходиться к реше­нию оптимизационной задачи .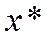

Определение 2. Пусть 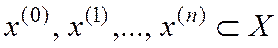- некоторая последователь­ность векторов из . Эта последовательность называется сходящей­ся по норме к элементу , если , т.е. если с ростом "расстояние" между элементами последовательности и вектором 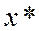становится сколь угодно малым.

Правило формирования последовательности

(1)

Вектор задает направление движения в пространстве ,

число - величину "шага" при переходе из точки в точку .

1. Как выбирать векторы 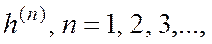чтобы обеспечить движение в направлении точки ?

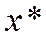2. Как выбирать числа чтобы двигаться к точке 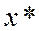достаточно (в каком-то смысле) быстро?

3. Как долго проводить вычисления по формуле (1), т.е. как узнать, что при некотором величина достаточно близка к , если неизвестно (иначе не было бы задачи)?

4. Как выбрать начальное приближение

Если используется информация только о целевой функции , алгоритм называют алгоритмом нулевого порядка; если используется информация о производных первого порядка - алгоритмом первого порядка; если используются вторые производные - алгоритмом второго порядка и т.д.

Если алгоритм за конечное число шагов приводит в точку , его называют конечношаговым, иначе - бесконечношаговым.

1. Выбор направление поиска

Оп ределение 3. Будем говорить, что вектор в точке задает направление убывания функции 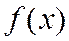(в задаче минимизации), если при всех достаточно ма­лых величинах 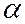выполняется условие . Такой вектор называют направлением убывания.

Множество всех направлений убывания функции 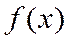в точке обо­значим через

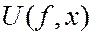
Утверждение 1. Вектор тогда и только тогда, когда

(2)

2. Правило выбора параметра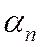

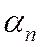
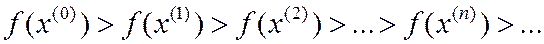(3)

Алгоритм (1) относят к методам спуска

а) ,

б) ,

в) (4)

г) (5)

(6)

Вычислительные процедуры типа (1) с (5), (6) называют алгоритмами наискорей­шего спуска

3. Скорость сходимости алгоритма

Определение 4. Пусть при . Тогда говорят:

· последовательность сходится к линейно (с линейной скоростью, со скоростью геометрической прогрессии), если и 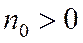такие, что

; (6а)

· последовательность сходится к сверхлинейно, если при такие, что

(6б);

· последовательность сходится к с квадратичной скоростью, если такие, что

(6в)

4. Правилами останова алгоритма

(7)

где - некоторые достаточно малые положительные числа.

5. Выбор точки начального приближения

2.4. Численные методы одномерной минимизации

Постановка задачи

Для функции одной переменной необходимые условия локальной оптимальности определяется следующими соотношениями:

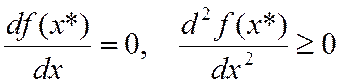(1)

Достаточное условие

(2)

Определение1. Пусть 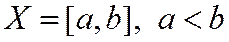. Одномерная действи­тельная функция 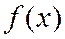называется унимодальной на , если существует такая точка , что

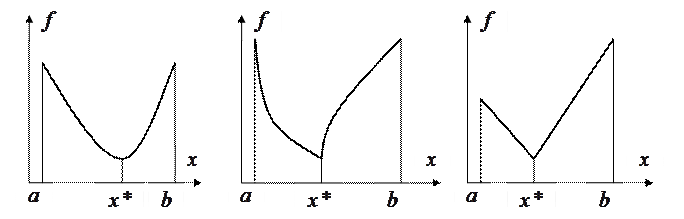
Рис. 1

Задача одномерной минимизации ставится следующим образом. Найти точку локального минимума унимодальной на отрезке целевой функции с абсолютной ошибкой . Формально эту задачу записывают так

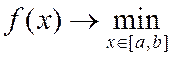(3)

Метод перебора

Идея метода состоит в переборе некоторого множества точек отрезка 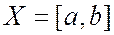и вычислении соответствующих значений целевой функ­ции. Точка с минимальным значением целевой функции объявляется ре­шением задачи (3).

· Отрезок 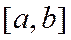разбивается на равных частей

(4)

точками деления

;

· вычисляются значения функции 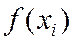в этих точках;

·

Искомая точка мини­мума

Точка минимума 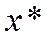локализована в отрезке

Отрезок локализации

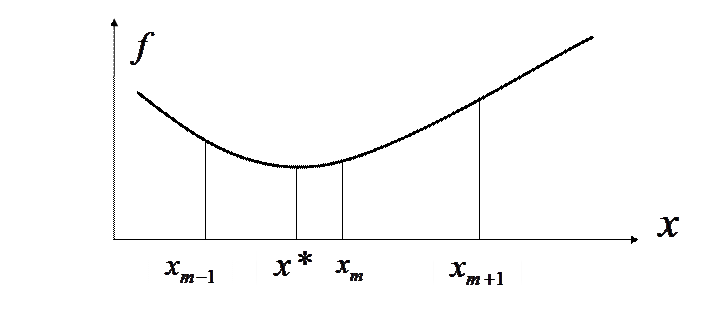
Рис. 2

Длина отрезка локализации

Абсолютная ошибка определения

.

Число вычислений значений ЦФ

2.5. Численные методы многомерной оптимизации

(1)

Метод конфигураций (метод Хука – Дживса) – представляет собой комбинацию «исследующего» поиска и ускоряющего поиска.

Метод нулевого порядка

Исследующий поиск ориентирован на выявление характера локального поведения ЦФ в окрестности точки приближения к оптимуму.

Полученная на этом этапе информация используются при проведении ускоряющего поиска

Дата добавления: 2015-07-25