Теорема 2

Пусть 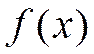- дважды непрерывно дифференцируемая функция в некоторой окрестности точки . Если - точка локального минимума (максимума) функции 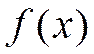, то матрица Гессе неотрицательно (неположительно) определена, т.е.

, (8)

где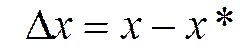

Теорема 3 Достаточное условие локальной оптимальности

Пусть 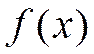- дважды непрерывно дифференцируемая функция в некоторой окрестности точки . Если удовлетворяет условию (2), а матрица Гессе положительно (отрицательно) определена, т.е.

, (9)

то - точка строгого локального минимума (максимума) функции .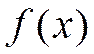

Замечания:

1. Каждое из условий (2) и (8) по отдельности, а также оба вместе, являются необходимыми, в то время, как только совокупность условий (2) и (9) является достаточным условием. Условие (2) называется необходимым условием I рода, условие (8) - необходимым условием II рода.

2. Условие (8) означает выпуклость (вогнутость) функции в некоторой окрестности точки . Условие (9) означает строгую выпуклость (вогнутость) функции в некоторой окрестности точки .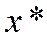

3. Из теорем вытекает, что если градиент целевой функции равен нулю и ее матрица Гессе положительно определена, то имеет место локальный минимум, если отрицательно определена, - локальный максимум.

Схема отыскания локального экстремума дважды непрерывно дифференцируемой функции:

1. Составляется система уравнений .

2. Находятся стационарные точки 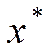функции.

3. Составляется матрица Гессе .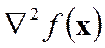

4. Для каждой стационарной точки 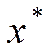вычисляется 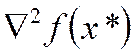, устанавливается ее знакоопределенность и делается вывод относительно наличия и квалификации экстремума (минимум это или максимум).

Дата добавления: 2015-07-25