
Читайте также:
|
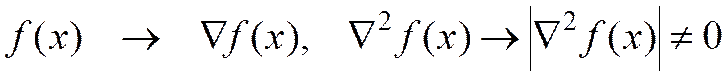 ,
,
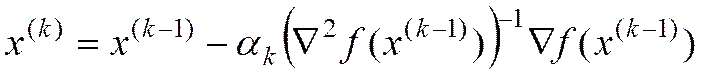
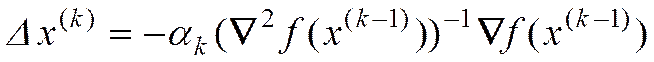 (6)
(6)
где 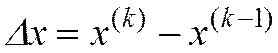 ;
;
Квазиньютоновский поиск:
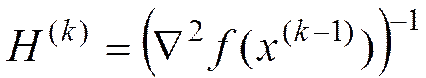
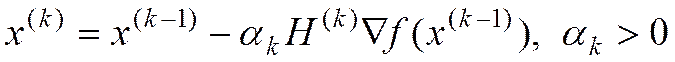 (7)
(7)
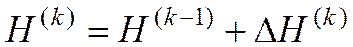 , (8)
, (8)
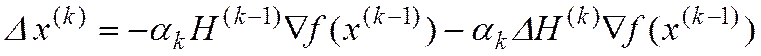 (9)
(9)
Эквивалентность матриц 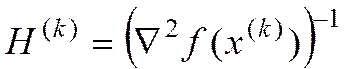 (6), (9)
(6), (9)
Если 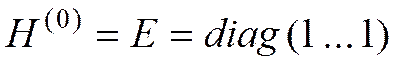 ,
,
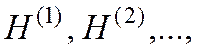 - симметрические и положительно определенные, то квазиньютоновский метод относится к методам спуска
- симметрические и положительно определенные, то квазиньютоновский метод относится к методам спуска
Практические вопросы безусловной оптимизации
Выбор метода
Самое общее правило: чем больше информации о производных будет использовано при решении задачи, тем лучше. При условии, что цена затрат будет приемлемой.
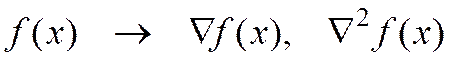
Матрица Гессе свободно помещается в ОЗУ 
В этой ситуации известные методы поиска минимума можно ранжировать следующим образом:
· ньютоновские методы;
· квазиньютоновские методы;
· методы сопряженных градиентов;
· методы сопряженных направлений нулевого порядка;
· градиентные методы;
· метод Хука - Дживса.
Оценка пригодности численного решения.
Тесты:
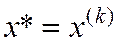
а) выполнено ли неравенство 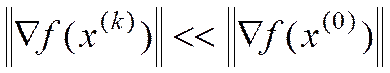 ?
?
б) достигнута ли на завершающих итерациях высокая скорость сходимости?
в) является ли матрица Гессе хорошо обусловленной?
а)
б) Скорость сходимости можно оценить по значениям разностей
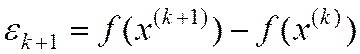
на нескольких последних итерациях.
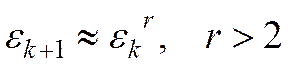 - квадратичная скорость сходимости;
- квадратичная скорость сходимости;
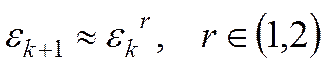 - сверхлинейная скорость сходимости
- сверхлинейная скорость сходимости
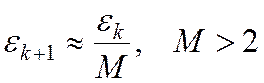 - предполагают линейную скорость сходимости к точке минимума ЦФ.
- предполагают линейную скорость сходимости к точке минимума ЦФ.
в) 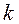 - итерация
- итерация 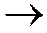 оценка точки минимума
оценка точки минимума 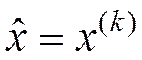
Близость оценки к искомой точке минимума можно определить нормой разности 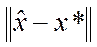
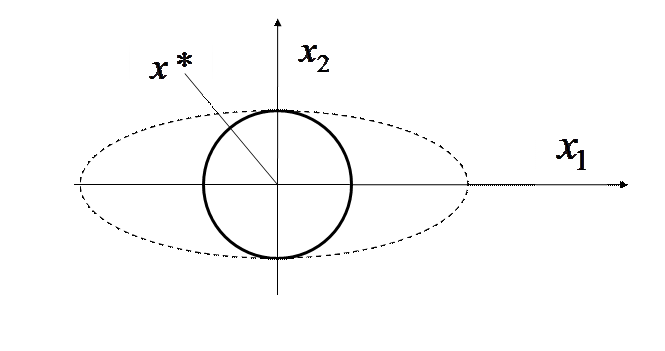
Обусловленность оптимизационной задачи определяется обусловленностью матрицы Гессе целевой функции
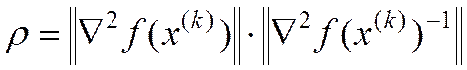 ,
,
число обусловленности матрицы 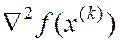
Обозначим через 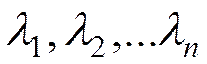 собственные числа матрицы Гессе, получаемые из уравнения
собственные числа матрицы Гессе, получаемые из уравнения
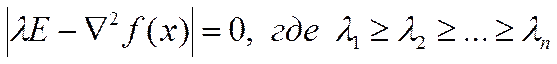 .
.
Тогда 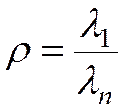 .
.
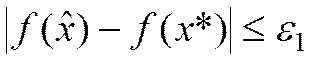 (1)
(1)
Любую точку, удовлетворяющую (1), можно называть решением задачи
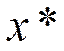 - точка строгого локального минимума,
- точка строгого локального минимума, 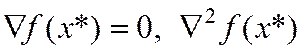 - положительно определенная матрица.
- положительно определенная матрица.
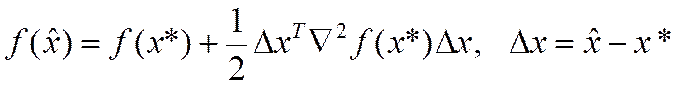 (2)
(2)
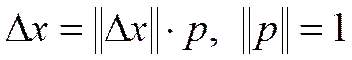
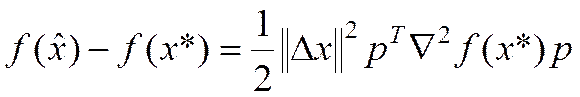
Отсюда следует
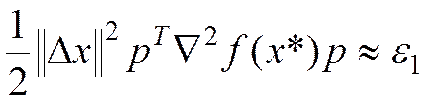 ,
,
что эквивалентно
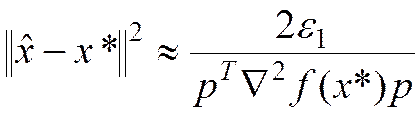 (3)
(3)
Пример. 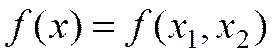 ,
,
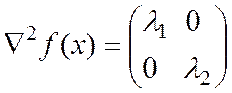 ,
, 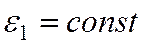
а)
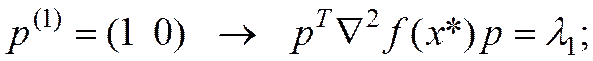
б)
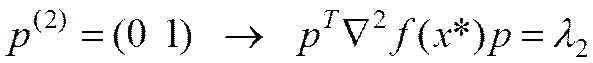
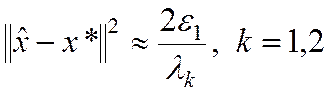 .
.
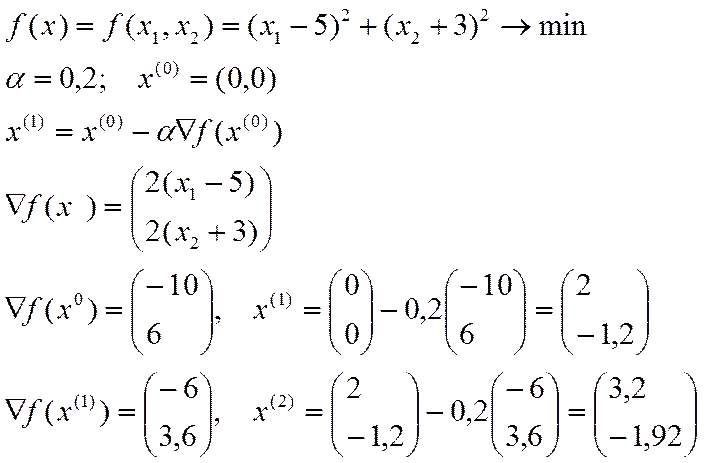
Дата добавления: 2015-07-25; просмотров: 79 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Метод Ньютона | | | Понятие о квазиньютоновских методах |