Вычислительная процедура

1. Выбирается точка ,

шаг для каждой переменной .

;

2. Проводится «исследующий» поиск в окрестности т.

2.1. Вычисляется ;

2.2. Каждая переменная поочередно изменяется путем добавления величины :

,

иначе

После перебора всех координат - «исследующий» поиск

завершается

2.3. Проверяется результативность «исследующего» поиска:

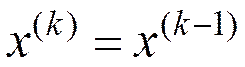- поиск признается неудачным п. 2.4.

переход к ускоряющему поиску п.3

2.4. Проверка условий окончания поиска () и ,

Если условия окончания поиска выполняются и

,

иначе п.2.1.

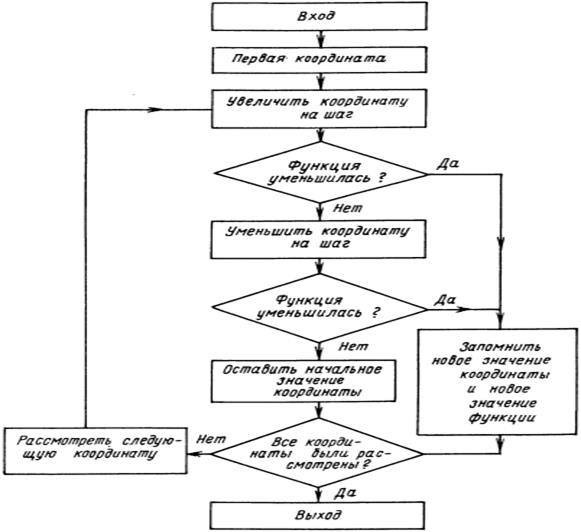
3. Осуществляется ускоряющий поиск

(2)

Если

(2)

Если

п.2.1

Особенности метода:

· несложная стратегия поиска;

· относительная простота, невысокие требования к объему памяти ЭВМ;

· из-за циклического движения по координатам может не сходится к точке минимума; в ряде случаев вырождается в последовательность исследующих поисков, что снижает эффективность процедуры минимизации;

· метод – бесконечношаговый.

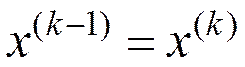
Градиентные методы поиска

Методы используют информацию о градиенте це­левой функции и относятся к методам первого порядка.

(3)

дифференцируема на

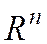
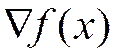
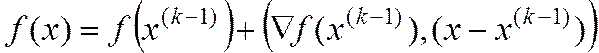(4)

(5)

Поскольку 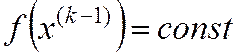, то

(6)

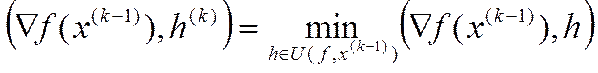(7)

Из свойства скалярного произведения

. (8)

- (9)

градиентные методы

,

(10)

Методы спуска

1. Простейший градиентный метод ;

2. Метод наискорейшего спуска

(11)

Из (11) следует:

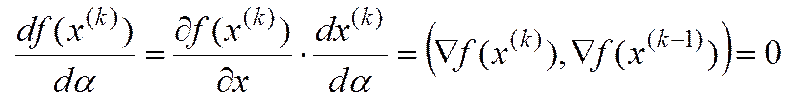
3. Градиентный метод с дроблением шага

3.1. часто ;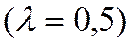

3.2. к следующей итерации

Особенности методов:

· относятся к локальным методам оптимизации;

· используются для решения как одномерных, так и многомерных экстремальных задач;

· выпуклая ЦФ – метод сходится к точке минимума;

сильно выпуклая ЦФ - метод сходится к точке минимума с линейной скоростью;

невыпуклая ЦФ - метод сходится ко множеству стационарных точек

· градиентные методы относятся к методам спуска ;

· низкая скорость сходимости в окрестности точки минимума; метод чувствителен к ошибкам вычислений; градиентные методы целесообразно применять на начальном этапе оптимизационной процедуры.

Дата добавления: 2015-07-25