Формула Резерфорда

Резерфорд вывел формулу для относительной доли частиц, рассеянных на угол, находящийся в интервале (q, q + d q):

,

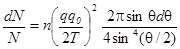здесь N - поток падающих частиц в пучке;

dN - поток рассеянных частиц

n - число ядер (атомов) в расчете на единицу поверхности

Т - кинетическая энергия налетающих частиц

q и q ₀ заряды налетающей частицы и ядра

Выражение 2p sinq d q - это телесный угол d W, в пределах которого заключены углы рассеяния (q, q + d q). Поэтому формулу Резерфорда можно переписать в виде:

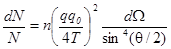
Проверка формулы Резерфорда.

Формула Резерфорда была подтверждена экспериментально. В качестве налетающих частиц использовали a-частицы (их заряд q = 2 e) от радиоактивного источника. Кинетическая энергия a-частиц была порядка нескольких МэВ.

Если зафиксировать телесный угол d W, в котором подсчитывают рассеянные a-частицы, и менять при этом угол q, то из формулы следует, что

dN × sin⁴(q/2) = const

На опыте, прежде всего, было проверено соблюдение именно этого условия. Оказалось, что, несмотря на то, что каждый из сомножителей в левой части последней формулы изменялся (в процессе изменения угла q) на три порядка, их произведение с хорошей точностью оставалось постоянным. Это означает, что формула Резерфорда правильно описывает процесс рассеяния a-частиц.

Итак, результаты опытов по рассеянию a-частиц говорят в пользу ядерной (планетарной) модели атома, предложенной Резерфордом. Однако эта модель оказалась в резком противоречии с законами классической электродинамики.

Предположение, что электроны движутся вокруг ядра по траекториям, подобно планетам вокруг Солнца, наталкивается на непреодолимую (с точки зрения классики) трудность. Двигаясь по искривленным траекториям, электрон испытывает ускорения, а, значит, неизбежно должен излучать электромагнитные волны. Этот процесс сопровождается потерей энергии, в результате чего электрон должен, в конечном счете, упасть на ядро. Время жизни такого атома оказывается порядка 10^-11 с. Этот результат красноречиво говорит о степени неустойчивости рассмотренной модели атома.

Дата добавления: 2015-07-11