Потенциальные барьеры

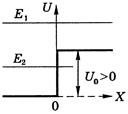
Рассмотрим простейший случай - прямоугольный потенциальный барьер, когда потенциальная энергия U зависит только от одной координаты х, причем при х = 0 претерпевает скачок (рисунок). У такого барьера

Пусть слева на границу барьера налетает с полной энергией Е частица или поток частиц. На языке квантовой теории это означает, что на барьер слева «падает» дебройлевская волна

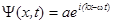
Чтобы удовлетворить граничным условиям для Y и ¶Y/¶ х при х = 0, должна существовать как прошедшая волна, так и отраженная волна. В этих трех волнах частота w одна и та же (w = Е / 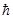), поэтому в дальнейших расчетах мы можем ограничиться только координатной частью этих волн, а именно y(х).

Наша задача: сначала найти амплитуды отраженной и падающей волн, а затем - коэффициенты отражения R и пропускания D для такого барьера. Исходим из уравнения Шредингера

В нашем случае оно имеет вид

(3)

Здесь возможны два случая (рисунок): E > U ₀ и E < U ₀.

1. В случае E > U ₀ общее решение (3) имеет вид:

Будем считать, что падающая волна характеризуется амплитудой а ₁, причем вещественной, а отраженная - амплитудой b ₁. В области х > 0 имеется только проходящая волна, поэтому b ₂ = 0. Из условия непрерывности y и в точке х = 0 следует, что

y₁(0) = y₂(0), или а ₁ + b ₁ = a ₂

¶y₁/¶ x = ¶y₂/¶ x, или a ₁ k ₁ + b ₁ k ₁ = a ₂ k ₂

Из совместного решения этих двух уравнений находим, что отношения амплитуд отраженной и прошедшей волн к амплитуде а ₁ падающей волны равны:

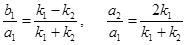
для определения интересующих нас коэффициентов R и D введем понятие плотности потока вероятности Р. Скорость распространения вероятности такого потока просто совпадает с классической скоростью v частицы, и мы можем написать v = p / m = 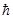k / m. Таким образом, v ~ k, и плотность потока вероятности пропорциональна величине k YY*:

P ~ k YY*

В соответствии с видом Y-функции для падающей, отраженной и прошедшей волн мы имеем

P ~ k ₁ , P ^/~ k ₁ , P ^// ~ k ₂

Теперь можно записать выражения для коэффициентов отражения R и пропускания D:

R = P ^//P; D = P ^// / P

Видим, что значения R и D не зависят от направления движения частицы: слева-направо или наоборот (рисунок).

В классическом случае R = 0 при E > U ₀

2. В случае E < U ₀ формулы 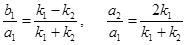остаются справедливыми. Однако будет чисто мнимым. При этом выражение для коэффициента отражения следует записать так:

Здесь числитель и знаменатель - величины комплексно-сопряженные. Значит R = 1, т.е. отражение частиц будет полным. Но Y-функция при х > 0 не обращается в нуль. В самом деле, полагая k ₂ = ik, где , получим, что

Отсюда плотность вероятности местоположения частицы

Р (х) = Р (0) е ^{-2 kx}

Видно, что с увеличением глубины проникновения х плотность вероятности Р (х) убывает экспоненциально. Это убывание происходит тем быстрее, чем больше разность (U ₀ - E). Обычно глубину проникновения определяют как расстояние l, на котором Р (х) убывает в е раз. При этом в формуле Р (х) = Р (0) е ^{-2 kx} 2 kl = 1 и

Можно убедиться, что для электрона при U ₀ - E» 10^-3 эВ глубина проникновения l» 10^-7 см.

Таким образом, Y-функция проникает в область х > 0, несмотря на то, что падающая волна отражается полностью.

В классической физике проникновение частиц под барьер запрещено, такого быть не может. Но в квантовой механике известно, что разделение полной энергии Е на кинетическую и потенциальную не совместимо с соотношением неопределенностей.

Дата добавления: 2015-07-11