Спектральные закономерности

В первую очередь нас будут интересовать спектры, обусловленные излучением невзаимодействующих друг с другом атомов. Эти спектры состоят из отдельных узких спектральных линий, и их называют линейчатыми. Наличие многих спектральных линий указывает на сложность внутреннего строения атома. Изучение атомных спектров послужило ключом к познанию внутренней структуры атомов. Прежде всего, было замечено, что спектральные линии расположены не беспорядочно, а образуют серии линий. Изучая линейчатый спектр атомарного водорода, Бальмер (1885 г.) установил следующую закономерность. В современных обозначениях она выглядит так:

, n = 3, 4, 5,...,

где w - циклическая частота, соответствующая каждой спектральной линии (w= 2p с /l), R - постоянная Ридберга:

R = 2,07 × 10¹⁶ с^-1

Формулу называют формулой Бальмера, а соответствующую серию спектральных линий - серией Бальмера (рисунок). Основные линии этой серии находятся в видимой части спектра.

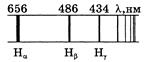
Дальнейшие исследования спектра атомарного водорода показали, что имеется еще несколько серий. В ультрафиолетовой части спектра - серия Лаймана:

, n = 2, 3, 4, 5,...,

а в инфракрасной части спектра - серия Пашена:

, n = 4, 5,...,

а также серии Брэкета и Пфунда.

Все эти серии можно представить в виде обобщенной формулы Бальмера:

, где n ₀ =1 для серии Лаймана, n ₀ =2 для серии Бальмера и т.д.

При заданном n ₀ число n принимает все целочисленные значения начиная с n ₀ + 1.

С ростом n частота линий в каждой серии стремится к предельному значению R / , которое называют границей серии (рисунок). За границей серии спектр не обрывается, а становится сплошным. Это присуще не только всем сериям водорода, но и атомам других элементов.

Дата добавления: 2015-07-11