Уравнение Шредингера

Поиск уравнения, управляющего изменениями состояния системы, т.е. ее Y-функции во времени успешно был завершен Э. Шредингером (1926 г.). Это - основное уравнение нерелятивистской квантовой теории, уравнение Шредингера. Данное уравнение было именно найдено, оно является новым фундаментальным законом, который невозможно вывести из прежних представлений и теорий. Справедливость этого уравнения установлена тем, что все вытекающие из него следствия подтверждены экспериментом.

Сформулировав это уравнение, Шредингер сразу же применил его к атому водорода и получил для уровней энергии спектр, точно совпадающий со спектром по первоначальной теории Бора и соответственно - с результатами наблюдений.

Уравнение Шредингера играет в квантовой теории такую же роль, как основное уравнение динамики (2-й закон Ньютона) в нерелятивистской механике.

Уравнение Шредингера имеет следующий вид:

,

где i - мнимая единица (), m - масса частицы, Ѳ - оператор Лапласа, U - потенциальная энергия (мы ограничимся рассмотрением потенциальных силовых полей, для которых функция U (r) не зависит явно от времени).

Обратим внимание на следующую особенность уравнения. В то время как, согласно интерпретации Y-функции, частица «размазана» в пространстве, потенциальная энергия U рассматривается как функция локализованной точечной частицы в силовом поле.

Стационарные состояния

Особую роль в квантовой теории играют стационарные состояния - состояния, в которых все наблюдаемые физические величины не меняются с течением времени. Сама Y-функция, как уже говорилось, принципиально ненаблюдаема. В стационарных состояниях она имеет вид

Y(r, t) = y(r) 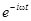, w = Е/ 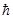, где функция y(r) не зависит от времени.

При таком виде Y-функции плотность вероятности Р остается постоянной. В самом деле,

Р = YY* = y(r) × y*(r)

т.е. действительно, плотность вероятности Р от времени не зависит.

Для нахождения функции y(r) в стационарных состояниях подставим выражение Y(r,t) = y(r) 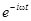в исходное уравнение

После сокращения получаем окончательно

(1)

Это уравнение называют уравнением Шредингера для стационарных состояний. В отличие от него, исходное уравнение называют временным или общим уравнением Шредингера.

Еще раз напомним, что потенциальная энергия - функция U (r) - здесь определяется классически, как если бы никакими волновыми свойствами частица не обладала.

Дата добавления: 2015-07-11