Гипотеза де-Бройля

Луи де-Бройль (1923 г.) высказал и развил идею о том, что материальные частицы должны обладать и волновыми свойствами. К тому времени уже сложилась парадоксальная, но подтвержденная опытом, ситуация о свете: в одних явлениях (интерференция, дифракция и др.) свет проявляет себя как волны, в других явлениях с не меньшей убедительностью - как частицы. Это и побудило де-Бройля распространить подобный корпускулярно-волновой дуализм на частицы с массой покоя, отличной от нуля.

Если с такой частицей связана какая-то волна, можно ожидать, что она распространяется в направлении скорости v частицы. О природе этой волны ничего определенного де-Бройлем не было высказано. Следует сразу подчеркнуть, что эти волны не электромагнитные. Они имеют специфическую природу, для которой нет аналога в классической физике.

Де-Бройль высказал гипотезу, что соотношение р = , относящееся к фотонам, имеет универсальный характер. Т.е. для всех частиц длина волны

l =

Эта формула получила название формулы де-Бройля, а l - дебройлевской длины волны частицы с импульсом р.

Де-Бройль также предположил, что пучок частиц, падающих на двойную щель, должен за ними интерферировать.

Вторым, независимым от формулы де Бройля соотношением является связь между энергией частицы и частотой w дебройлевской волны:

Е =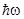

С частотой w и волновым числом k = 2p/l связаны две скорости - фазовая v_ф и групповая u:

v_ф = и

Посмотрим, как эти скорости связаны с величинами, характеризующими состояние частицы. Для этого выпишем сначала формулы, связывающие волновые и корпускулярные свойства частиц

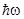= Е; = = р

Ограничимся рассмотрением только нерелятивистского случая. Учтем, что в этом случае кинетическая энергия связана с импульсом частицы соотношением Е = р ²/2 m.

Умножим числитель и знаменатель обеих выражений для скорости на 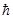и учтем предыдущие формулы:

v_ф = , u =

Из второй формулы следует, что групповая скорость дебройлевских волн равна скорости частицы.

Из первой формулы следует, что фазовая скорость дебройлевских волн

v_ф

т.е. зависит от частоты w, а, значит, дебройлевские волны обладают дисперсией даже в вакууме.

Установление того факта, групповая скорость дебройлевских волн равна скорости частицы, сыграло в свое время важную роль в развитии принципиальных основ квантовой физики, и в первую очередь в физической интерпретации дебройлевских волн. Сначала была сделана попытка рассматривать частицы как волновые пакеты весьма малой протяженности и таким образом решать парадокс двойственности свойств частиц. Однако подобная интерпретация оказалась ошибочной, так как все составляющие пакет гармонические волны распространяются с разными фазовыми скоростями. При наличии большой дисперсии, свойственной дебройлевским волнам даже в вакууме, волновой пакет «расплывается». Для частиц с массой порядка массы электрона пакет расплывается практически мгновенно, в то время как частица является стабильным образованием.

Таким образом, представление частицы в виде волнового пакета оказалось несостоятельным. Проблема двойственности свойств частиц требовала иного подхода к своему решению.

Выясним, в каких явлениях могут проявляться волновые свойства частиц. Мы знаем, что независимо от природы волн - это интерференция и дифракция. Непосредственно наблюдаемой величиной в них является длина волны. Во всех случаях дебройлевская длина волны определяться формулой l= . Проведем с помощью нее некоторые оценки.

Прежде всего, убедимся, что гипотеза де-Бройля не противоречит понятиям макроскопической физики. Возьмем в качестве макроскопического объекта, например, пылинку, считая, что ее масса m = 1мг и скорость v = 1 мкм/с. Соответствующая ей длина волны l = 7 × 10^-20 см. Т.е. даже у такого небольшого макроскопического объекта как пылинка дебройлевская длина волны оказывается неизмеримо меньше размеров самого объекта. В таких условиях никакие волновые свойства, конечно, проявить себя не могут.

Иначе обстоит дело, например, у электрона с кинетической энергией Т и импульсом р = . Его дебройлевская длина волны 1,22/ 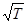нм, где Т в эВ. При Т =150 эВ дебройлевская длина волны электрона равна l» 0,1 нм. Такой же порядок величины имеет постояная кристаллической решетки. Поэтому кристаллическая структура может быть подходящей решеткой для получения дифракции дебройлевских волн электронов.

Дата добавления: 2015-07-11