Состояние частицы в квантовой теории

Рассмотрение вопроса о математическом формализме, адекватном парадоксальному поведению микрочастиц, мы начнем с выяснения принципов, на которых строится фундаментальная физическая теория. Проследим за содержанием этих принципов в классической и квантовой теории на простейшем примере движения нерелятивистской частицы в стационарном силовом поле.

Для этого должны быть определены:

1) величины, задающие состояние частицы;

2) уравнение движения, определяющее изменение состояния частицы во времени;

3) физические величины, доступные измерению, и способ получения их значений в данном состоянии (это необходимо для сравнения выводов теории с экспериментом).

Обратимся сразу к решению этих вопросов в квантовой теории.

Для микрочастиц из-за соотношения неопределенностей классическое определение состояния частицы (координаты и импульс), вообще говоря, утрачивает смысл. Это относится и к понятию силы, которая по определению является функцией классического состояния. В соответствии с корпускулярно-волновым дуализмом в квантовой теории состояние частицы задается пси-функцией Y(r, t), которая является комплексной величиной и формально обладает волновыми свойствами.

Понимание физического смысла пси-функции пришло после того, как выяснилось, что волновые свойства характерны для отдельных частиц. Этот факт можно истолковать по идее Борна (1926 г.) так. Движение любой микрочастицы по отдельности подчиняется вероятностным законам. Распределение вероятности, характеризующее это движение, проявляется в результате регистрации достаточно большого числа частиц. Это распределение оказывается таким же, как распределение интенсивности волны: там, где интенсивность волны больше, регистрируется большее число частиц.

В квантовой теории постановка вопроса состоит не в точном предсказании событий, а в определении вероятностей этих событий. По значениям вероятностей согласно определенным правилам можно найти средние случайных значений физических величин, которые и доступны эксперименту. Пси-функция Y(r, t) и является той величиной. которая позволяет находить все вероятности. Например, вероятность нахождения частицы в интересующем нас объеме dV в момент t определяется как

dP = |Y| ² dV = YY* dV

где Y* - комплексно-сопряженная функция, отсюда плотность вероятности, т.е. вероятность нахождения частицы в единице объема,

Р = |Y| ² = YY*

Эта величина является экспериментально наблюдаемой, в то время как сама пси-функция, будучи комплексной, не доступна наблюдению.

Пси-функция, вообще говоря, определяется с точностью до произвольного постоянного множителя. Это не влияет на состояние частицы, которое она описывает. И, тем не менее, пси-функцию выбирают так, чтобы она удовлетворяла условию нормировки:

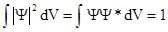
где интеграл берется по всему пространству или по той области, в которой Y отлична от нуля. Условие нормировки означает, что по всей области, где Y¹0, частица находится с достоверностью. Пси-функцию, удовлетворяющую вышеприведенному условию называют нормированной.

Принцип суперпозиции

Итак, непосредственный физический смысл имеет не сама Y-функция, а квадрат ее модуля |Y| ² или YY*. И тем не менее в квантовой теории оперируют с Y-функцией, а не с экспериментально наблюдаемой величиной |Y|². Это необходимо для истолкования волновых свойств микрочастиц - интерференции и дифракции. Ситуация здесь совершенно идентична той, какую мы имеем в волновой теории. В волновой теории принимается принцип суперпозиции самих волновых полей, а не их интенсивностей. Именно так вводятся в теорию явления интерференции и дифракции.

Подобным же образом в квантовой теории принимается как один из основных постулатов принцип суперпозиции пси-функций. Если у некоторой системы возможными являются состояния Y₁ и Y₂, то для нее существует также состояние

Y = с ₁Y₁ + с ₂Y₂,

где с ₁ и с ₂ - некоторые постоянные коэффициенты. Найдя таким образом Y, можно далее определить и плотность вероятности YY* пребывания системы в этом состоянии.

Подтверждение принципа суперпозиции является согласие с опытом вытекающих из него следствий.

Дата добавления: 2015-07-11