Определение перемещений от внешней нагрузки в статически неопределимых стержневых системах

При расчете вагонных конструкций приходится определять перемещения отдельных точек системы. Как правило, эти перемещения малы по сравнению с размерами системы или ее элементов. По найденным перемещениям оценивают жесткость системы.

Таким образом, умение определять перемещения точек стержневой системы необходимо не только при ее расчете методом сил, но и при расчете на жесткость.

При определении перемещений, вызываемых внешней нагрузкой, используется формула (3.11), которая применима как для статически определимых, так и статически неопределимых систем.

С целью упрощения рассмотрим определение перемещений с учетом только деформации изгиба, т.е. с учетом первого слагаемого формулы.

В статически определимой стержневой системе перемещение какой-либо ее точки (точки К) определяется как результат перемножения эпюры моментов от внешней нагрузки 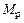на эпюру моментов от единичной силы, приложенной в точке, перемещение которой надо найти:

. (3.26)

Например, найдем перемещение точки К в горизонтальном направлении для рамы, приведенной на рисунке 3.31, а.

Эпюры моментов от заданной внешней нагрузки и от единичной силы показаны на рисунках 3.31, б, в.

Тогда, перемещение точки К рамы

.

В статически неопределимых системах для построения эпюры моментов от внешней нагрузки требуется раскрыть статическую неопределимость и построить окончательную суммарную эпюру от заданной нагрузки, как это делается при расчете систем методом сил. В случае приложения к статически неопределимой системе единичной силы требуется повторно произвести расчет, т. е. снова раскрыть статическую неопределимость и построить окончательную эпюру моментов от воздействия единичной силы.

Рисунок 3.31 – К определению горизонтального перемещения точки К статически определимой системы:

а – исходная система; б, в – эпюры моментов от внешней нагрузки и единичной силы

Следовательно, для определения перемещения в статически неопределимой системе необходимо дважды раскрывать статическую неопределимость, что увеличивает трудоемкость расчета. Однако, при выполнении практических расчетов этого не требуется.

Рассмотрим простейшую статически неопределимую систему в виде однопролетной балки (рисунок 3.32, а). На рисунках 3.32, б, в показаны эпюры моментов – окончательная М от заданной нагрузки и окончательная единичная от единичной силы Р = 1, полученные в результате расчета статически неопределимой балки.

Тогда, перемещение точки К балки

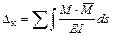. (3.27)

Перемножение эпюр дает следующий результат:

.

Рассмотрим, как можно упростить расчет.

Если отбросить в заданной системе лишние связи, превратив ее в статически определимую, и приложить к полученной основной системе заданную нагрузку и реакции отброшенных связей, то окончательная эпюра М не изменится. Причем независимо от выбранного варианта основной системы.

На рисунках 3.32, г, е показаны эпюры окончательных изгибающих моментов для двух вариантов основных систем, загруженных внешней нагрузкой и реакциями связей. В обоих случаях эпюры изгибающих моментов М одинаковы и не отличаются от эпюры, приведенной на рисунке 3.32, б. Отличает их от заданной системы то, что для построения эпюр использовались статически определимые системы.

Рисунок 3.32 – К определению вертикального перемещения точки К статически

неопределимой системы:

а – исходная система; б, в – эпюры М и для заданной статически неопределимой системы; г-д – эпюры М и для первого и второго вариантов основной системы

Поскольку деформации заданной и полученных из нее статически определимых систем одинаковы, то перемещения точки К можно вычислить в статически определимой системе. Для таких систем эпюру моментов от единичной силы построить достаточно просто (рисунки 3.32, д, ж).

Тогда, перемещение точки К:

для первого варианта основной системы (рисунки 3.32, г, д) –

;

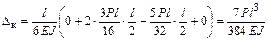для второго варианта основной системы (рисунки 3.32, е, ж) –

.

Как следует из выполненных расчетов, искомое перемещение точки К для всех трех рассмотренных случаев одинаково. Однако, использование при определении перемещения эпюры , построенной в статически определимой системе, существенно упрощает расчет.

Таким образом, при определении перемещения точки К эпюра М должна быть построена для заданной статически неопределимой системы, а эпюра – для статически определимой системы, полученной из заданной удалением лишних связей.

П р и м е ч а н и е – При построении эпюры 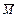может быть использована любая основная система

В качестве статически определимой системы выбирается система, в которой проще строить эпюру от единичной силы и выполнять перемножение эпюр.

В приведенных вариантах основных систем более простым для построения эпюры является вариант на рисунке 3.32, д, поскольку в рассматриваемом случае эпюра располагается не по всей длине балки и имеет нулевой участок.

П р и м е ч а н и е – Результат определения перемещения точки К не изменится, если эпюра будет построена для статически неопределимой системы, а эпюра 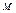– для статически определимой.

Рассмотрим расчет горизонтального перемещения точки К для рамы, изображенной на рисунке 3.30, а.

Расчет рамы приведен в п. 3.9. Окончательная эпюра моментов М, полученная по результатам расчета, показана на рисунке 3.30, ж.

Для построения эпюры используем основную систему, приведенную на рисунке 3.33, а. Хотя можно было бы использовать и прежнюю основную систему (см. рисунок 3.30, б). Эпюра показана на рисунке 3.33, б.

Перемножая эпюры М и , получим

.

П р и м е ч а н и е – Знак минус означает, что точка К перемещается в направлении, обратном направлению единичной силы Р, т.е. влево.

Рисунок 3.33 – К определению горизонтального перемещения точки К статически неопределимой системы: а – исходная система; б – эпюра моментов от единичной силы

Дата добавления: 2015-07-10