Статически неопределимых стержневых вагонных конструкций

Особенности расчета:

· в сечениях пространственной стержневой системы (см. рисунок 3. 22) действуют в общем случае загружения 6 внутренних силовых факторов (изгибающие моменты и , крутящий момент , поперечные силы и , нормальная сила N);

· в сечениях плоскопространственной стержневой системы, которая является частным случаем пространственной системы, сохраняются только силовые факторы, плоскость действия которых перпендикулярна плоскости рамы (, , ). Силовые факторы, лежащие в плоскости рамы, равны нулю.

В качестве примера рассмотрим расчет рамы тележки пассажирского вагона модели 68-875 (рисунок 3.44). Рама образована совокупностью балок: двух продольных боковых 1 со шпинтонами 5, четырех вспомогательных продольных 2, двух средних поперечных 3 и четырех укороченных концевых 4.

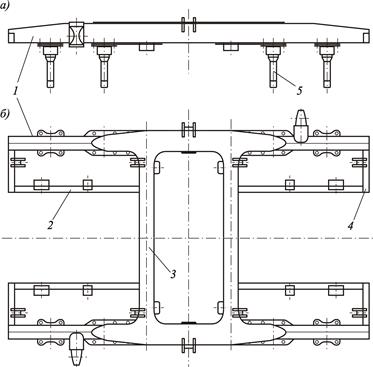
Рисунок 3.44 – Рама тележки пассажирского вагона:

а – вид сбоку; б – вид сверху

Исходная расчетная схема. Конструктивная схема рамы показана на рисунке 3.45, а. Расчетная схема рамы создается линиями, проходящими через центры тяжести поперечных сечений ее балок. Поскольку балки рамы расположены не в одной плоскости, то расчетная схема будет пространственной. В то же время, если оси балок рамы будут смещены одна относительно другой на сравнительно небольшую величину, то расчетную схему можно принять плоской, располагая осевые линии балок в плоскости боковых.

В расчетную схему можно не включать вспомогательные продольные балки 2, к которым крепятся детали тормозной рычажной передачи, ввиду их малой жесткости по сравнению с жесткостью по сравнению с жесткостью боковых балок.

Таким образом, при построении расчетной схемы вводятся следующие допущения:

расчетная схема принимается плоской;

вспомогательные продольные балки в расчетную схему не вводятся в виду их малой жесткости.

Расчетная схема рамы, учитывающая введенные допущения, приведена на рисунке 3.45, б.

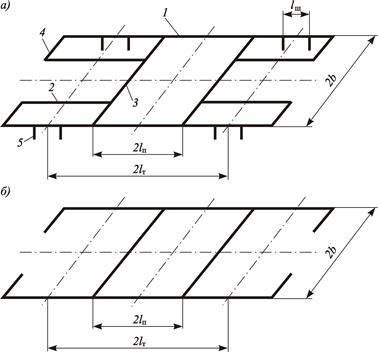
Рисунок 3.45 – Схема рамы тележки пассажирского вагона:

а – конструктивная; б – расчетная

Данная расчетная схема пригодна для расчета на все нагрузки (вертикальные и горизонтальные), кроме тормозных.

Степень статической неопределимости заданной системы. Расчетная схема такой рамы в общем случае загружения внешними силами шесть раз статически неопределима, так как она имеет один замкнутый контур и пространственное загружение.

Рассмотрим расчет рамы методом сил строительной механики.

Выбор основной системы. Основную систему в данном случае создаем с использованием жестких консолей и упругого центра путем:

рассечения правой поперечной балки по продольной оси симметрии;

присоединения в местах разреза абсолютно жестких консолей, оканчивающихся в упругом центре;

переноса лишних неизвестных Х ₁, Х ₂,..., X ₆ в упругий центр.

Полученная рациональная основная система приведена на рисунке 3.46. Для большей наглядности показано раздельное загружение ее внутренними силовыми факторами Х ₁, Х ₂, X ₃ и Х ₄, Х ₅, X ₆, действующими соответственно в плоскости рамы (рисунок 3.46, а) и перпендикулярно плоскости рамы (рисунок 3.46, б).

Рисунок 3.46 – Основная система, с внутренними силовыми факторами,

действующими:

а – в плоскости рамы; б – перпендикулярно плоскости рамы

Составление канонических уравнений. В результате введения жестких консолей получаем систему канонических уравнений с полностью разделенными неизвестными:

;

;

;

;

.

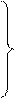
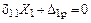Тогда

.

Определение коэффициентов и свободных членов канонических уравнений. Для определения 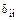и следует построить эпюры моментов от неизвестных силовых факторов Х ₁ = 1, …, X ₆ = 1 и внешней нагрузки и перемножить их по правилам перемножения эпюр.

Единичные эпюры моментов от Х ₁ = 1, …, X ₆ = 1 показаны на рисунке 3. 47.

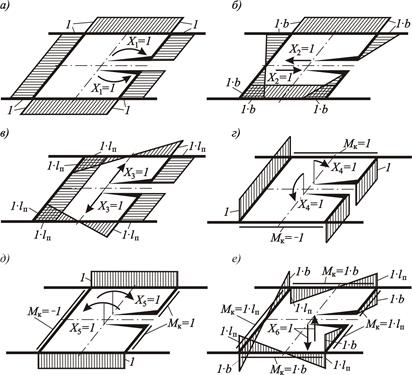
Рисунок 3.47 – Единичные эпюры изгибающих и крутящих моментов:

а – от ; б – от ; в – от ; г – от ; д – от ; е – от

П р и м е ч а н и е – При построении эпюры М каждый элемент рамы нужно рассматривать как отдельный стержень, защемленный одним концом.

Напомним также, что при переносе силы F параллельно самой себе из одной точки в другую, нужно уравновесить перенесенную силу такой же силой, но направленной в другую сторону. Тогда в точке переноса будут действовать перенесенная сила и момент (от пары сил F).

При построении грузовой эпюры необходимо учитывать, что на раму действуют различные внешние силы в двух плоскостях: в плоскости рамы и перпендикулярно плоскости рамы. Поэтому нужно определиться с внешней силой, от воздействия которой будет рассчитываться рама.

Грузовые эпюры для различных внешних расчетных сил будут приведены ниже.

Коэффициенты 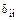и свободные члены вычисляем по формулам перемножения эпюр с учетом деформаций:

· изгиба в горизонтальной плоскости – от неизвестных Х ₁, Х ₂, X ₃, действующих в плоскости рамы –

;

;

· изгиба в вертикальной плоскости и кручения – от неизвестных Х ₄, Х ₅, X ₆, действующих перпендикулярно плоскости рамы –

;

,

где , 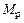– изгибающие моменты в основной системе соответственно от действия силового фактора и от внешней нагрузки;

, – то же крутящие моменты;

, – жесткость стержней соответственно на изгиб относительно нейтральных осей z и y;

– то же на кручение.

Расчетные нагрузки. Внешние силы, учитываемые при расчете рамы, действуют в двух плоскостях: в плоскости рамы и перпендикулярно плоскости рамы (рисунок 3.48).

Как известно, при смешанной нагрузке, действующей на плоскую раму, всегда имеется возможность разложить силы по плоскостям и рассмотреть отдельно плоскую и плоскопространственную системы. Внутренние силовые факторы определяются как результат наложения полученных решений.

Напомним также, что несимметричную нагрузку, действующую в каждой плоскости, можно разложить на симметричные и кососимметричные составляющие.

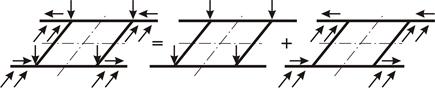
Рисунок 3.48 – Разложение внешней нагрузки по плоскостям

Рассмотрим расчет рамы тележки на действие вертикальных нагрузок – кососимметричной и симметричной .

В этом случае получаем плоскопространственную систему, в которой будут возникать силовые факторы Х ₄, Х ₅ и X ₆.

Расчет рамы на вертикальную составляющую от боковых сил. Данная нагрузка – вертикальная составляющая от боковых сил – будет прикладываться к раме в четырех точках (в точках крепления подвесок люльки), перпендикулярно плоскости рамы. Причем дальняя боковая балка будет загружаться двумя сосредоточенными силами 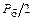, а передняя – разгружаться такими же двумя силами.

Рассматриваемая нагрузка является кососимметричной (антисимметричной) по отношению к продольной оси симметрии.

Опорами рамы являются пружины буксовых рессорных комплектов, т.е. имеем 8 опорных реакций.

Грузовая эпюра 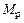от воздействия внешних сил показана на рисунке 3. 49.

Таким образом, мы имеем симметричную раму, на которую действует внешняя нагрузка, кососимметричная относительной продольной оси. Тогда в сечениях рамы, расположенных на продольной оси симметрии, симметричный силовой фактор Х ₄ равен нулю, т.е. в сечении будут действовать 2 силовых фактора Х ₅ и X ₆.

Следовательно, рассматриваемая система два раза статически неопределима и канонические уравнения имеют вид

Коэффициенты 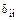и свободные члены вычисляем по формулам, учитывающим деформации изгиба в вертикальной плоскости и кручения.

Неизвестные силовые факторы

; .

Ординаты окончательной эпюры изгибающих и крутящих моментов

;

;

где , , 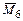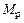– эпюры изгибающих моментов соответственно от силовых факторов Х ₅ = 1, X ₆ = 1 и внешней нагрузки;

, , – то же эпюры крутящих моментов.

Рисунок 3.49 – Эпюры изгибающих и крутящих моментов от вертикальных

нагрузок, обусловленных действием боковых сил

Значения ординат этих эпюр используются для расчета нормальных, касательных и эквивалентных напряжений в сечениях рамы, т.е. для оценки прочности рамы.

Расчет рамы на вертикальную статическую нагрузку. Вертикальная статическая нагрузка будет прикладываться к раме в точках крепления подвесок люльки в виде четырех сосредоточенных сил . Опорами рамы являются пружины буксовых рессорных комплектов.

Рассматриваемая нагрузка является симметричной относительной продольной и поперечной осей симметрии.

Грузовая эпюра 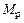от воздействия внешней нагрузки приведена на рисунке 3.50.

Рисунок 3.50 – Эпюры изгибающих моментов от вертикальной статической

нагрузки, окончательной в заданной системе

Учет симметричности конструкции и загружения рамы позволяют упростить расчет. Как известно, в сечениях рамы, расположенных на продольной оси симметрии, кососимметричные силовые факторы Х ₅ и X ₆ равны нулю.

Это означает, что рассматриваемая система один раз статически неопределима и каноническое уравнение имеет вид

.

Учитываем также, что свободный член (результат перемножения эпюр и 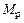с нулевыми участками по всем стержням) равен нулю. Следовательно, .

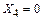Отсутствие лишнего неизвестного при загружении рамы нагрузкой указывает на то, что заданная система является статически определимой (внутренние усилия от рассматриваемой нагрузки статически определимы) и ординаты эпюры изгибающих моментов 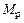от рассматриваемой нагрузки являются окончательными.

Дата добавления: 2015-07-10