Решение системы канонических уравнений

Определение коэффициентов и свободных членов канонических уравнений. Для определения реакци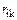й и необходимо предварительно построить эпюры моментов в основной системе: единичные – от неизвестных единичных перемещений и грузовую 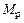– от внешней нагрузки.

П р и м е ч а н и е – Строятся только эпюры изгибающих моментов, поскольку при расчете рам методом перемещений пренебрегают влиянием продольных и поперечных сил на деформации стержней.

Как уже отмечалось, введенные связи превращают основную систему в совокупность простых статически неопределимых стержней (балок). В нашем случае, стержней АВ, ВС и СD (см. рисунок 4.7). Причем каждый из них работает самостоятельно.

П р и м е ч а н и е – Самостоятельная работа стержня означает, что если, например, на стержень АВ действует внешняя нагрузка Р, то от этой нагрузки будет деформироваться только этот стержень. Другие стержни в этом случае не изгибаются.

Эпюры моментов строятся индивидуально для каждого стержня основной системы по справочным данным, приведенным в таблице 4.1, в зависимости от схемы его закрепления и воздействия на него (действие нагрузки или кинематическое воздействие – поворот или смещение узлов). Тогда эпюры моментов в основной системе для рамы в целом (как от внешней нагрузки, так и от единичных смещений) представляют собой совокупность эпюр, построенных для отдельных стержней.

П р и м е ч а н и е – Единичные эпюры в методе перемещений строятся от кинематического воздействия.

В рассматриваемом случае необходимо построить единичные эпюры 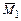(от поворота угловой связи (заделки) 1 на угол 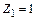), 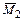(от поворота угловой связи (заделки) 2 на угол 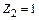), 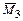(от линейного смещения связи (стержня) 3 на 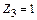) и грузовую эпюру 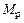(от внешней нагрузки Р).

Для определения реакци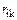й и можно использовать два способа: статический и перемножения эпюр.

В методе перемещений основным является статический способ, что объясняется его простотой. Он основан на использовании уравнений равновесия для определения реакций введенных связей.

Как известно, реакции (реактивные усилия) 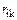и могут быть двух типов:

реактивные моменты (в угловых связях);

реактивные силы (в линейных связях).

Реактивные моменты во введенных заделках определяются путем вырезания узлов из соответствующих эпюр ( или 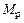) и составления уравнения равновесия вида .

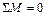П р и м е ч а н и е – Вырезаются только узлы, содержащие «плавающие» заделки.

Реактивные усилия во введенных стержнях определяются путем вырезания отдельных частей рамы и составления уравнения равновесия вида .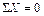

Особенности построения эпюр и определения реакци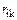й и рассмотрим в п. 4.6.

Проверка правильности вычисления коэффициентов канонических уравнений метода перемещений производится аналогично проверке, выполняемой при расчете методом сил (см. п. 3.5), т.е. проверяется выполнение условия

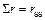, (4.3)

где 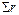– сумма всех найденных коэффициентов при неизвестных,

;

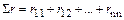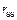– перемещение, получаемое умножением эпюры саму на себя.

Проверка правильности вычисления свободных членов канонических уравнений заключается в проверке выполнимости условия

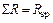, (4.4)

где 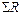– сумма всех свободных членов,

;

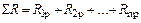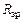– перемещение, получаемое перемножением эпюр 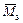и ,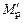

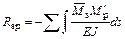; (4.5)

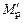– эпюра изгибающих моментов от внешней нагрузки в любой основной статически определимой системе метода сил, полученной из заданной системы.

П р и м е ч а н и е – Как следует из формулы (4.5), для определения 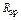необходимо перемножить эпюры 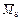и 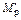и знак результата изменить на обратный.

Решение системы канонических уравнений. Найденные значения коэффициентов и свободных членов (реакци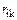й и ) подставляют в канонические уравнения. Решают полученную систему уравнений относительно неизвестных с помощью ЭВМ, используя стандартную программу решения линейных алгебраических уравнений.

Дата добавления: 2015-07-10