Выбор симметричной основной системы

Симметричная основная система – основная система, в которой неизвестные силовые факторы размещаются по оси симметрии.

В симметричной основной системе получаем основные неизвестные в виде симметричных и кососимметричных силовых факторов.

Рассмотрим некоторое произвольное сечение, в котором под воздействием внешней нагрузки возникают 6 силовых факторов (рисунок 3.22).

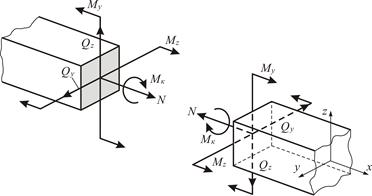
Рисунок 3.22 – Силовые факторы, возникающие в произвольном сечении рамы

В правой и левой плоскостях произведенного сечения силы и моменты равны, но направлены в разные стороны.

Под симметричными силовыми факторами понимают такие, которые образуют зеркальное отображение относительно плоскости сечения. Силовые факторы, каждый из которых противоположен по знаку зеркальному отображению взаимного фактора, являются кососимметричными.

Тогда, на рисунке 3.22:

, , N – симметричные силовые факторы;

, , – кососимметричные силовые факторы.

Симметричные силовые факторы дают симметричные эпюры, а кососимметричные – кососимметричные эпюры. Т.е. получаем взаимно нулевые эпюры.

Правило 1. Коэффициенты канонических уравнений 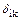, у которых один индекс принадлежит симметричному фактору, а другой – кососимметричному фактору, обращаются в нуль. И их сразу можно вычеркнуть из системы канонических уравнений.

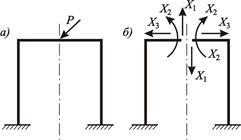
Рассмотрим симметричную раму (рисунок 3.23, а).

Рисунок 3.23 – Упрощение расчета рамы с помощью выбора симметричной основной системы: а – исходная система; б – симметричная основная система

Система канонических уравнений для этой рамы в общем случае нагружения будет иметь вид:

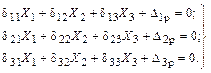(3.24)

Симметричная основная система для рассматриваемой рамы показана на рисунке 3.23, б.

В приведенной основной системе: Х ₁ – кососимметричный силовой фактор; Х ₂, Х ₃ – симметричные силовые факторы.

В соответствии с правилом 1: 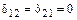и .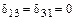

Тогда, система канонических уравнений (3.24) будет иметь вид:

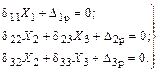(3.25)

В результате система из трех уравнений распадается на две независимые системы, одна из которых относится к симметричным силовым факторам, другая – к кососимметричным. Решение двух систем проще, чем решение полной системы.

Таким образом, выбор симметричной основной системы позволяет решение системы из n уравнений с n неизвестными заменить решением двух независимых систем. Это сокращает объем вычислений.

П р и м е ч а н и я:

1 Если заданная система является симметричной, то и основную систему надо всегда выбирать симметричной.

2 Выбор симметричной основной системы позволяет получить основные неизвестные в виде симметричных и кососимметричных силовых факторов, которые дают соответственно симметричные и кососимметричные эпюры.

3 В результате обращения в нуль коэффициентов канонических уравнений с индексами, принадлежащими симметричным и кососимметричным силовым факторам, происходит распад полной системы уравнений на две независимые системы.

Дата добавления: 2015-07-10