
Читайте также:
|
Степень статической неопределимости системы равна числу лишних (избыточных) связей, которые следует удалить из статически неопределимой системы для обращения ее в статически определимую и геометрически неизменяемую.
П р и м е ч а н и е – Связи условно называют лишними вследствие того, что они не являются безусловно необходимыми для обеспечения неизменяемости системы
Различают системы с внешней или внутренней статической неопределимостью. В первом случае лишними являются внешние (опорные) связи (рисунки 3.1, а, б), во втором – внутренние (рисунок 3.1, в). Система может быть также внешне и внутренне статически неопределимой (рисунок 3.1, г).
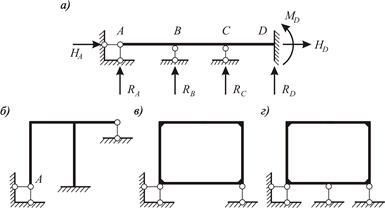
Рисунок 3.1 – Статически неопределимые системы:
а, б – с лишними внешними связями; в – с лишними внутренними связями; г – с лишними внешними и внутренними связями
Рассмотрим два основных способа определения числа лишних связей в системе.
Первый способ – аналитический. Основывается на сопоставлении числа связей в системе с числом степеней свободы.
Число лишних связей внешне статически неопределимой системы (балки или рамы) вычисляется с использованием формулы:
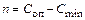 , (3.1)
, (3.1)
где  – общее число опорных стержней системы;
– общее число опорных стержней системы;
 – число стержней, необходимых для обеспечения геометрической неизменяемости и неподвижности системы, для плоских систем
– число стержней, необходимых для обеспечения геометрической неизменяемости и неподвижности системы, для плоских систем  .
.
Например, для трехпролетной балки, изображенной на рисунке 3.1, а,  ; для двухпролетной рамы (рисунок 3.1, б)
; для двухпролетной рамы (рисунок 3.1, б)  .
.
Число лишних связей системы, состоящей из дисков, может быть определено исходя из формулы (2.2) и равно степени свободы системы 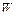 , взятой с обратным знаком:
, взятой с обратным знаком:
 . (3.2)
. (3.2)
Для рам, показанных на рисунках 3.2, а – в, число лишних связей составляет соответственно:
 ;
;  ;
;  .
.
В последнем случае (рисунок 3.2, в) рама представляет собой бесшарнирный замкнутый контур и содержит три лишние связи. В этом легко убедится, отбросив одну из опор рамы и заменив удаленные связи их реакциями (рисунок 3.2, г). В результате получим геометрически неизменяемую и неподвижную систему.
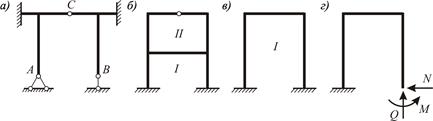
Рисунок 3.2 – К расчету числа лишних связей
Формула (3.2) справедлива лишь в том случае, когда все диски системы являются системами без лишних связей (статически определимы). В противном случае необходимо учитывать статическую неопределимость дисков.
Например, для прямоугольной рамы (см. рисунок 3.1, в), представляющей замкнутый контур, число лишних связей по формуле (3.2) составит –  . Однако, это не означает, что система не имеет лишних связей. В действительности она имеет три лишних внутренних связи. Для превращения ее в статически определимую систему (консольную балку ломаного очертания) необходимо разрезать один из стержней и тем самым удалить три внутренние связи (рисунок 3.3). Удаленные связи должны быть заменены их реакциями – N, Q и M.
. Однако, это не означает, что система не имеет лишних связей. В действительности она имеет три лишних внутренних связи. Для превращения ее в статически определимую систему (консольную балку ломаного очертания) необходимо разрезать один из стержней и тем самым удалить три внутренние связи (рисунок 3.3). Удаленные связи должны быть заменены их реакциями – N, Q и M.
Таким образом, любой бесшарнирный замкнутый контур, независимо от его формы и расположения в системе, трижды статически неопределим, т.е. содержит три лишние связи.
Введем в замкнутый контур шарнир (рисунок 3.4). В разрезе, проведенном по этому шарниру, будут действовать только два внутренних усилия N и Q. Следовательно, такой контур имеет две лишние связи, т.е. дважды статически неопределим.
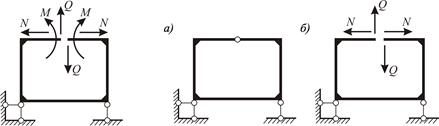
| Рисунок 3.3 – К расчету числа лишних связей для замкнутого бесшарнирного контура | Рисунок 3.4 – К расчету числа лишних связей для замкнутого контура с шарниром: а – исходная система; б – внутренние усилия, действующие в разрезе по шарниру |
Введение в раму простого шарнира снимает одну связь (разрешает поворот одного сечения относительно другого) и снижает общую степень статической неопределимости системы на единицу.
П р и м е ч а н и е – Шарнир может быть введен в любое место – на стержень или в узел рамы.
Число лишних связей системы, имеющей замкнутые контуры, удобно определять по формуле:
 , (3.3)
, (3.3)
где К – число замкнутых контуров системы (в предположении отсутствия шарнирных соединений);
Ш – число простых шарниров системы (число врезанных шарниров с учетом их кратности).
Формула (3.3) является основной для определения степени статической неопределимости рам.
П р и м е ч а н и я
1 В формула (3.3) учитывается, что каждый замкнутый бесшарнирный контур имеет три лишние связи, а каждый простой шарнир, введенный в такой контур, снимает одну связь, снижая степень статической неопределимости на единицу.
2 При расчете по формуле (3.3) рассматриваются шарниры (соединительные и опорные), эквивалентные простым. Напомним, что шарниры бывают простые и сложные. Простой шарнир соединяет два стержня, сложный – более двух (см. рисунки 2.5, а, б).
Сложный шарнир эквивалентен (n – 1) простым шарнирам, где n – число соединяемых стержней. Для использования формулы (3.3) необходимо каждый сложный шарнир заменить эквивалентным числом простых шарниров, используя выражение Ш = n – 1.
3 При установлении кратности опорных шарниров следует исходить из следующего:
· шарнирно-неподвижную опору (рисунок 3.5) можно изображать в виде одного шарнира, связывающего систему с землей. Земля здесь выступает в роли абсолютно жесткого стержня;
· в шарнирно-подвижной опоре, имеющей два шарнира, шарнир, связывающий опорный стержень с землей, всегда является простым.
На рисунках 3.6, а, б, в показаны варианты присоединения стержней системы к шарнирно-неподвижной и шарнирно-подвижной опорам. Кратность опорных шарниров обозначена цифрами.

Рисунок 3.5 – Схематическое изображение шарнирно-неподвижной опоры

Рисунок 3.6 – Варианты присоединения стержней системы к опорам:
а, б – шарнирно-неподвижной; в – шарнирно-подвижной
Поясним применение формулы (3.3). Для рам, показанных на рисунках 3.2, б и 3.4, а, число лишних связей составляет  и
и  (здесь и далее римскими цифрами обозначены номера контуров). Для рам на рисунках 3.1, в и 3.2, в
(здесь и далее римскими цифрами обозначены номера контуров). Для рам на рисунках 3.1, в и 3.2, в  . Полученные результаты совпадают с приведенными ранее.
. Полученные результаты совпадают с приведенными ранее.
Рассмотрим возможность использования формулы (3.3) для рамы, приведенной на рисунке 3.2, а.
Для получения бесшарнирных замкнутых контуров предполагаем, что опоры А и В являются жесткими заделками, а шарнир С отсутствует (рисунок 3.7, а). В результате имеем три контура I, II и III. Далее представим, что в рассматриваемую раму с тремя бесшарнирными замкнутыми контурами введены шарниры – соединительный и опорные. При этом, шарнирно-неподвижную опору А показываем в виде одного шарнира. Рама с введенными шарнирами, показана на рисунке 3.7, б. Кратность шарниров обозначена цифрами. В рассматриваемой системе имеем Ш = 4.
Тогда 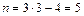 , что совпадает с полученным ранее результатом.
, что совпадает с полученным ранее результатом.
Рассмотрим теперь раму, изображенную на рисунке 3.8.

| Рисунок 3.7 – К получению бесшарнирных замкнутых контуров системы: а – система с замкнутыми контурами; б – система с введенными шарнирами | Рисунок 3.8 – К расчету числа лишних связей рамы |
Эту раму можно представить, состоящей из трех замкнутых контуров с введенными в нее двумя простыми и двумя сложным шарнирами. Каждый сложный шарнир эквивалентен двум простым. Кратность шарниров показана на схеме цифрами.
Число лишних связей системы –  .
.
Число лишних связей шарнирно-стержневых систем удобно определять исходя из формулы (2.3):
 . (3.4)
. (3.4)
Так, для шарнирно-стержневой системы, приведенной на рисунке 2.12, в,
 .
.
Второй способ определения числа лишних связей. Основывается на сопоставлении числа неизвестных усилий  в системе (числа связей в системе) с числом независимых уравнений статики
в системе (числа связей в системе) с числом независимых уравнений статики 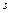 , которые можно составить для рассматриваемой системы.
, которые можно составить для рассматриваемой системы.
Число лишних связей системы в этом случае может быть определено из выражения
 . (3.5)
. (3.5)
Рассмотрим балку, изображенную на рисунке 3.1, а. Число неизвестных опорных реакций рамы равно 7, число уравнений статики для плоскости – 3, следовательно,  .
.
В практических расчетах стержневых систем удобно выражать число неизвестных усилий  через число стержней С системы, а число уравнений статики
через число стержней С системы, а число уравнений статики 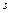 – через число узлов У.
– через число узлов У.
Тогда, число лишних неизвестных для стержневых систем:
· с шарнирными узлами –
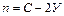 ; (3.6)
; (3.6)
· с жесткими узлами –
 ; (3.7)
; (3.7)
· с жесткими и шарнирными узлами –
 . (3.8)
. (3.8)
П р и м е ч а н и е – В формулах (3.6) – (3.8) учитывается, что:
· в стержне с шарнирными узлами неизвестным является одно усилие (N), с жесткими узлами – три усилия (M, N, Q);
· для каждого шарнирного узла можно составить два уравнения статики ( ,
,  ), для жесткого узла – три уравнения статики (
), для жесткого узла – три уравнения статики ( ,
,  ,
,  );
);
· каждый простой шарнир приводит к появлению дополнительного уравнения статики и понижает степень статической неопределимости на единицу.
Рассмотрим шарнирно-стержневую систему, изображенную на рисунке 2.12, в.
П р и м е ч а н и е – При определении числа лишних неизвестных для систем с шарнирными узлами по формуле (3.6) под числом стержней С понимают общее число стержней системы, включая опорные.
Для рассматриваемой системы с учетом примечания С = 24, У = 10.
Число лишних связей 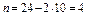 . Результат расчета совпадает с тем, что был получен для этой же системы при расчете по формуле (3.4).
. Результат расчета совпадает с тем, что был получен для этой же системы при расчете по формуле (3.4).
Далее определим число лишних неизвестных для рамы с жесткими узлами, которая показана на рисунке 3.9, а.
П р и м е ч а н и е – При определении числа лишних неизвестных для систем с жесткими узлами по формуле (3.7) в число узлов У системы не включаются опорные узлы, поскольку в каждое из уравнений равновесия для этих узлов войдут три опорные реакции и дополнительных уравнений для вычисления усилий в стержнях не при этом не появится.
С учетом примечания число узлов У = 6, С = 10.
Число лишних связей системы –  .
.
Аналогичный результат получим при использовании формулы (3.3), учитывая наличие четырех замкнутых контуров и отсутствие шарниров (Ш = = 0):  .
.
Рассмотрим определение числа лишних связей для рам с жесткими и шарнирными узлами, приведенных на рисунках 3.8 и 3.9, б. Кратность шарниров показана на схемах цифрами.

Рисунок 3.9 – К расчету числа лишних связей системы:
а – рама с жесткими узлами; б – рама с жесткими и шарнирными узлами
П р и м е ч а н и е – При расчете по формуле (3.8) в общее число узлов У системы не включаются опорные и учитывается кратность узлов.
Число лишних связей систем:  ;
;  .
.
Для рамы, изображенной на рисунке 3.8, результат аналогичен полученному ранее по формуле (3.3).
Обратим внимание на то, что число лишних неизвестных (степень статической неопределимости) будет зависеть от способа приложения внешней нагрузки.
Например, для балки с заделками по концам:
· для произвольно приложенной силы Р (рисунок 3.10, а) –
m = 6, 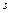 = 3 (
= 3 (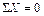 ,
,  ,
,  ),
),  ;
;
· для вертикальной силы Р (рисунок 3.10, б) –
m = 4, 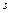 = 2 (
= 2 ( ,
,  ),
),  ;
;
· для горизонтальной силы Р (рисунок 3.10, в) –
m = 2, 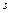 = 1 (
= 1 (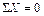 ),
), 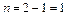 .
.
|

Дата добавления: 2015-07-10; просмотров: 926 | Нарушение авторских прав