|
Читайте также: |
При использовании способа преобразования нагрузки лишние неизвестные целесообразно располагать на оси симметрии системы.
Правило 2. Любую несимметричную нагрузку, действующую на симметричную раму, можно разложить на симметричную и кососимметричную составляющие (рисунок 3.24).
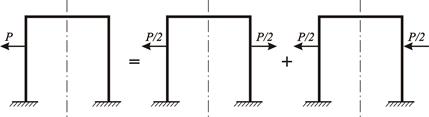
Рисунок 3.24 – Представление несимметричной нагрузки в виде суммы
симметричной и кососимметричной составляющих
Расчет выполняется отдельно на действие каждой из них. Результирующая эпюра, например, моментов получается путем алгебраического суммирования ординат двух эпюр
,
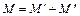где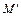 
, 
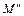– окончательные эпюры изгибающих моментов от действия симметричной и кососимметричной нагрузки соответственно.
Для несимметричной нагрузки при симметричной основной системе будут верны уравнения (3.25).
Правило 3. При симметричной внешней нагрузке, действующей на симметричную раму, кососимметричные силовые факторы, (
, 
, 
) в плоскости симметрии обращаются в нуль.
В соответствии с правилом 3: Х 1 = 0.
Тогда, уравнения (3.25) можно записать в виде
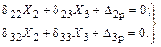
Правило 4. При кососимметричной внешней нагрузке, действующей на симметричную раму, симметричные силовые факторы (
, 
, N) в плоскости симметрии обращаются в нуль.
В соответствии с правилом 4: Х 2 = Х 3 = 0.
Следовательно, уравнения (3.25) можно будет записать в виде:
.
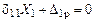П р и м е ч а н и е – Сущность рассмотренного способа упрощения расчета симметричной статически неопределимой системы состоит в разложении несимметричной нагрузки на симметричную и кососимметричную составляющие. Поскольку расчет на каждую составляющую нагрузки производится раздельно, то вместо одной системы уравнений с полным числом неизвестных получаем де независимые системы, одна из которых содержит только симметричные силовые факторы, другая – кососимметричные.
Правило 5. Расчет симметричной многопролетной рамы, на которую действует симметричная или кососимметричная внешняя нагрузка, можно упростить, рассматривая половину рамы – при одной оси симметрии и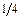 
часть рамы – при двух осях симметрии.
В местах разреза вводятся связи, соответствующие тем силовым факторам, которые возникают в сечении.
Рассмотрим трехпролетную симметричную раму, загруженную симметричной нагрузкой (рисунок 3.25, а) и кососимметричной (рисунок 3.26, а). Рама девять раз статически неопределима.
На рисунках 3.25, б и 3.26, б приведены упрощенные расчетные схемы 1/2 части рамы для рассматриваемых вариантов нагружения.
Действие отброшенной части на оставшуюся учитывается введением соответствующих опорных закреплений (связей).
|
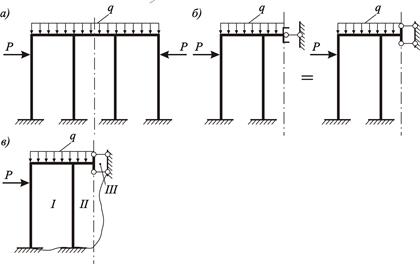
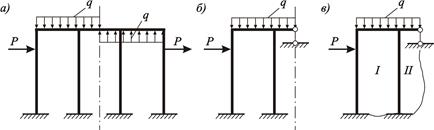
Рисунок 3.26 – Упрощение расчета симметричной рамы, загруженной
кососимметричной нагрузкой:
а – исходная система; б – 1/2 часть рамы; в – схема для расчета числа лишних неизвестных
1/2 части рамы
На расчётной схеме 1/2 части рамы, загруженной симметричной нагрузкой (см. рисунок 3.25, б), квадратной скобкой и горизонтальным стержнем с шарнирами по концам обозначены связи, закрепляющие сечение соответственно от поворотов в вертикальной плоскости и горизонтальных перемещений, т.е. от перемещений по направлению ненулевых внутренних усилий, которые возникают в сечении по оси симметрии.
Связи, закрепляющие сечения от вертикальных перемещений, не показаны, так как поперечные силы в плоскости симметрии равны нулю (правило 3).
При действии на раму кососимметричной нагрузки в месте разреза рамы введена связь в виде вертикального стержня с шарнирами по концам, закрепляющего сечение от вертикальных смещений (см. рисунок 3.26, б). Связи, соответствующие изгибающему моменту и нормальной силе, в плоскости симметрии равны нулю (правило 4).
Степень статической неопределимости 1/2 части рамы для рассматриваемых вариантов загружения снижается соответственно до пяти и четырех.
На рисунках 3.25, в и 3.26, в приведены схемы, поясняющие расчет степени статической неопределимости 1/2 части рам, с использованием формулы (3.3). Римскими цифрами на схемах обозначены номера контуров.
Рассматриваемый способ уменьшения степени статической неопределимости системы широко используется при расчете стержневых вагонных конструкций.
П р и м е ч а н и я:
1 Симметричность конструкции в сочетании с симметричностью или кососимметричностью внешней нагрузки позволяют уменьшить степень статической неопределимости системы за счет рассмотрения 1/2 или 1/4 части конструкции.
2 При выделении 1/2 или 1/4 части конструкции действие отброшенной части на оставшуюся компенсируется введением в местах разреза связей от ненулевых силовых факторов. При действии симметричной нагрузки на оси симметрии вводятся связи от симметричных силовых факторов, при действии кососимметричной нагрузки – от кососимметричных силовых факторов.
3 Выделенная 1/2 или 1/4 части конструкции с приложенной к ней внешней нагрузкой и введенными связями, рассматривается как самостоятельная расчетная схема.
Дата добавления: 2015-07-10; просмотров: 429 | Нарушение авторских прав