|
Читайте также: |
Исходная расчетная схема. Конструктивная схема боковой рамы показана на рисунке 3.34. Рассмотрим ее расчет на вертикальные силы, симметрично расположенные относительно ее продольной и поперечной вертикальных плоскостей симметрии.
К ним относятся следующие вертикальные силы: статическая Р ст, динамическая Р д и вертикальная составляющая от центробежной силы Р ц.
Тогда, суммарная вертикальная расчетная сила на боковую раму
.
Указанная расчетная сила передается на нижний горизонтальный пояс рамы рессорным комплектом. В типовой тележке рессорный комплект состоит из семи 2-рядных пружин, поэтому загружение боковой рамы можно представить в виде семи сосредоточенных сил, каждая из которых равна (l/7) P.
Расчетная схема боковой рамы принимается плоской стержневой. Она образуется линиями, проходящими через центры тяжести поперечных сечений ее стержней (см. рисунок 3.34).
Рисунок 3.34 – Боковая рама тележки и ее расчетная схема
В плоской расчетной схеме силы должны располагаться в плоскости рамы, поэтому на нижний горизонтальный пояс рамы будут действовать пять (а не семь – как в реальной конструкции) сосредоточенных сил: две крайние Р 1, две промежуточные Р 2 и средняя Р 1, причем Р 1 = (1/7) Р, Р 2 = (2/7) Р, т.е.
.
Опорные реакции прикладываются к серединам буксовых проемов рамы. Каждая из них принимается равной 0,5 Р.
Исходная информация для расчета. Выполним расчет боковой рамы 2-осной тележки грузового вагона с осевой нагрузкой 240 кН. Расчетные силы в этом случае будут иметь следующие значения: Р ст = 226,92 кН, Р д = 118,67 кН, Р ц. = 40,66 кН, Р = 386,25 кН, Р 1 = 55,18 кН, Р 2 = 110,36 кН, опорные реакции Р /2 = 193,125 кН.
Геометрические параметры расчетной схемы боковой рамы даны в таблице 3.1.
Таблица 3.1– Геометрические параметры расчетной схемы рамы тележки
грузового вагона*
| Обозначение | Значение | Обозначение | Значение |
| l 1 | 0,305 | 
| 0,166 |
| l 2 | 0,275 | 
| 0,017 |
| l 3 | 0,310 | t 1 | 0,123 |
| l 4 | 0,228 | t 2 | 0,377 |
Окончание таблицы 3.1
| Обозначение | Значение | Обозначение | Значение |
| l 5 | 0,297 | t 3 | 0,329 |
| l 6 | 0,095 | t 4 | 0,055 |
| l 7 | 0,105 | h 1 | 0,120 |
| l 8 | 0,105 | h 2 | 0,090 |
| c 1 | 0,150 | h 3 | 0,110 |
| c 2 | 0,209 | h 4 | 0,080 |
| d 1 | 0,167 | h 5 | 0,080 |
| d 2 | 0,075 | s | 0,187 |
| k 1 | 0,055 | r | 0,383 |
| k 2 | 0,330 | m | 0,620 |
| k 3 | 0,204 | n 1 | 0,562 |
| k 0 | 0,534 | n 2 | 0,363 |
| e 1 | 0,058 | l т | 0,925 |
| e 2 | 0,048 | z 1 | 0,715 |
| e 3 | 0,066 | z 2 | 0,820 |
| 0,195 | 
| 4o |
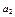
| 0,185 |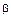 
| 55o |
| * Линейные размеры приведены в метрах, углы – в градусах |
В таблице 3.2 приведены геометрические характеристики сечений стержней (площади поперечных сечений F i и моменты инерции сечений J i, где i – номер стержня), которые приняты в качестве характерных для стержней рамы.
Таблица 3.2 – Геометрические характеристики сечений стержней рамы
| Номер стержня | F i·10-4, м2 | J i·10-8, м4 |
| 143,6 | ||
| 45,4 | ||
| 56,8 | ||
| 41,4 | ||
| 48,1 |
Упрощение расчетной схемы. Симметричность конструкции и загружения боковой рамы относительно вертикальной поперечной плоскости, проходящей через середину рамы, позволяет рассматривать 1/2 часть боковой рамы. Действие отброшенной части на оставшуюся учитывается введением соответствующих связей.
На расчётной схеме 1/2 части рамы (рисунок 3.35) квадратными скобками и стерженьками с шарнирами по концам обозначены связи, закрепляющие сечения соответственно от поворотов в вертикальной плоскости и горизонтальных перемещений. Связи, закрепляющие сечения от вертикальных перемещений, не показаны, так как поперечные силы в плоскости симметрии равны нулю. Расчетная схема 1/2 части рамы загружена вертикальными силами Р 1, Р 2, 0,5 Р 1 и уравновешивающей их реакцией 0,5 Р.
Особенностью конструкции боковой рамы, отличающей ее от обычных стержневых рам, является соизмеримость длин стержней с размерами их поперечных сечений. Эта особенность конструкции учитывается при построении расчетной схемы выделением в ней узлов (утолщенные линии на рисунках 3.34 и 3.35), которые принимают абсолютно жесткими на сдвиг.
Рисунок 3.35 – Расчетная схема ½ части боковой рамы
Установление степени статической неопределимости заданной системы. Расчетная схема всей боковой рамы состоит из трех замкнутых контуров и в общем случае загружения силами, действующими в плоскости рамы, девять раз статически неопределима. В стержнях боковой рамы возникают при этом деформации изгиба в вертикальной плоскости, растяжения-сжатия и сдвига.
Степень статической неопределимости 1/2 части рамы снижается до пяти, учитывая симметричность конструкции и загружения относительно вертикальной поперечной плоскости.
Рассмотрим расчет рамы методом сил строительной механики.
Выбор основной системы. Основную систему получают из расчетной схемы, устраняя лишние связи в средних сечениях верхнего горизонтального и наклонного поясов и вводя взамен удаленных связей их реакции 
, 
, …, 
(рисунок 3.36).
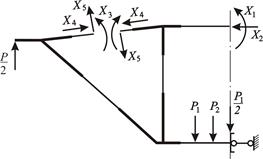
Рисунок 3.36 – Основная система
Составление канонических уравнений. Система канонических уравнений для определения неизвестных , , …, будет иметь вид:
Определение коэффициентов и свободных членов канонических уравнений. Для вычисления коэффициентов 
и свободных членов 
построим эпюры изгибающих моментов и продольных сил от неизвестных единичных силовых факторов , , …, и внешней нагрузки (рисунки 3.37 и 3.38) и затем перемножим их по правилам перемножения эпюр.
П р и м е ч а н и е – Коэффициенты 
и свободные члены 
будем определять как перемещения, обусловленные деформацией изгиба и растяжения-сжатия. Деформации сдвига с целью упрощения расчета не учитываем. Это несущественно сказывается на результатах расчета.
Рисунок 3.37 – Эпюры изгибающих моментов и нормальных сил:
а – от 
; б – от 
; в – от 
Рисунок 3.38 – Эпюры изгибающих моментов и нормальных сил:
а – от 
; б – от 
; в – от внешней нагрузки
При построении эпюр учитывается некоторая податливость узлов рамы. Эпюры моментов и продольных сил в теле узла считаются затухающими по линейному закону на длине, равной высоте поперечного сечения стержня. На участках стержней, расположенных между узлами, эти эпюры строят обычными методами.
Для удобства будем вычислять коэффициенты и свободные члены, увеличенные в Е раз.
Рассмотрим определение коэффициентов 
, 
и свободного члена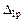 
.
Коэффициент 
определяем умножением эпюры 
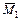на :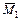
;
.
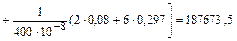Коэффициент находим, перемножив единичные эпюры М и N от Х 4 = 1 на эпюры от Х 5 = 1:
;
.
Свободный член определяем умножением эпюры 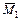на эпюру 
:
,
где 
;
;
;
.
.
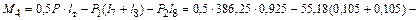
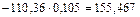
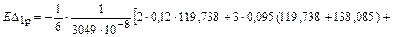
Значения остальных коэффициентов и свободных членов приведем без расчета:
; 
;
; 
;
;
; 
; 
;
;
; 
; 
;
; 
.
Для проверки полученных коэффициентов и свободных членов строим суммарные единичные эпюры 
и 
от совместного действия сил 
, 
, …, 
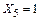(рисунок 3.39).
Умножая эпюры и сами на себя, а также на эпюру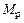 
, получим:
.
.
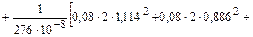
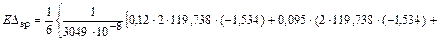
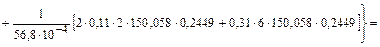
Рисунок 3.39 – Суммарные единичные эпюры:
а – изгибающих моментов; б – продольных сил
Определяем сумму коэффициентов 
и свободных членов 
канонических уравнений:
;
.
Поскольку 
, а расхождение между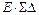 
и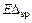 
практически близко к нулю, коэффициенты и свободные члены определены правильно.
Решение системы канонических уравнений. Подставляем полученные значения коэффициентов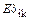 
и свободных членов 
в систему канонических уравнений. Сокращаем на Е и решаем уравнения относительно неизвестных , , …, . Для вычисления используем стандартную программу для решения линейных алгебраических уравнений.
Результаты расчета:
; 
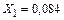
кН; 
;
кН; 
кН.
Построение окончательных эпюр моментов и продольных сил. Ординаты окончательных эпюр изгибающих моментов и продольных сил для рассматриваемого случая
Вычисление ординат окончательных эпюр М и N выполняем в табличной форме (таблицы 3.2 и 3.3).
При этом учитываем знаки силовых факторов 
, а также моментов и продольных сил.
Таблица 3.2 – Вычисление ординат окончательной эпюры М
| Номер стержня | Номер сечения | Х 1 = 0,084 кН·м | Х 2 = 242,149 кН | Х 3 = 1,514 кН·м | |||
| 
| 
| 
| 
| 
| ||
| 1а 2а | –1 –1 –1 –1 | –0,084 –0,084 –0,084 –0,084 | –0,534 –0,534 –0,534 –0,534 | –129,308 –129,308 –129,308 –129,308 | – – – – | – – – – | |
| 0,084 0,084 | 0,330 0,055 | 79,909 13,318 | –1 –1 | –1,514 –1,514 | |||
| – – | – – | – – | – – | –1 –1 | –1,514 –1,514 | ||
| – – | – – | – – | – – | 1,514 1,514 | |||
| 0,084 0,084 | – – | – – | – – | – – |
Окончание таблицы 3. 2
| Номер стержня | Номер сечения | Х 4 = –216,835 кН | Х 5 = –13,151 кН | 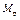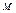 , кН·м
|  , кН·м
| ||
| 
| 
| 
| ||||
| 1а 2а | – – – – | – – – – | – – – – | – – – – | 119,738 138,085 152,570 155,467 | –9,654 8,693 23,178 26,075 | |
| 0,329 0,055 | –71,339 –11,926 | 0,166 0,185 | –2,183 –2,433 | – – | 4,957 –2,471 | ||
| 0,123 0,377 | –26,671 –81,747 | –0,195 –0,017 | 2,564 0,234 | 36,114 73,967 | 10,493 –9,060 | ||
| – – | – – | 0,114 –0,114 | –1,499 1,499 | – – | 0,015 3,013 | ||
| – – | – – | – – | – – | – – | 0,084 0,084 |
Таблица 3.3 – Вычисление ординат окончательной эпюры N
| Номер стержня | Х 1 = 0,084 кН·м | Х 2 = 242,149 кН | Х 3 = 1,514 кН·м | |||
| 
| 
| 
| 
| 
| |
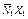
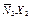
| – – – – – | – – – – – | – – – –1 | 242,149 – – – –242,149 | – – – – – | – – – – – |
Окончание таблицы 3.3
| Номер стержня | Х 4 =-216,835 кН | Х 5 = -13,151 кН | 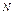 , кН
|  , кН·
| ||
| 
| 
| 
| |||
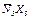
| – –0,0697 –0,5740 – | – 15,113 124,463 –216,835 – | – –0,9976 0,8189 – – | – 13,119 –10,769 – – | – – 150,058 – – | 242,149 28,232 263,722 –216,835 –242,149 |
Окончательные эпюры М и N показаны на рисунке 3.40.
Значения ординат этих эпюр используются для оценки прочности боковой рамы.
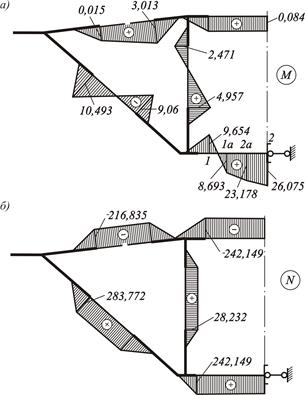
Рисунок 3.40 – Окончательные эпюры:
а – изгибающих моментов; б – продольных сил
Дата добавления: 2015-07-10; просмотров: 843 | Нарушение авторских прав