Введение жестких консолей

Этот способ применяется для рам, имеющих замкнутый контур (см. рисунки 3.1, в и 3.2, в), и позволяет получать системы канонических уравнений с полностью разделенными неизвестными

Рассмотрим систему, показанную на рисунке 3.1, в.

В случае выбора традиционной симметричной основной системы (рисунок 3.29, а) для нее будет справедлива система уравнений (3.25), в которой – кососимметричный силовой фактор, , 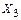– симметричные силовые факторы.

Тогда, побочные коэффициенты 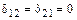и .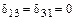

В полученных уравнениях все побочные коэффициенты, кроме коэффициентов 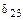и 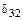равны нулю, т.е. .

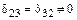Для получения системы уравнений с полностью разделенными неизвестными необходимо также обратить в нуль и коэффициенты 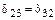с индексами, принадлежащими симметричным факторам.

Коэффициенты 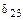и 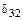являются результатом перемножения единичных эпюр 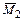и .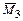

Для ортогонализации (обращения в нуль) этих эпюр необходимо перенести неизвестные в точку C, называемую упругим центром, с помощью жестких консолей.

П р и м е ч а н и е – При наличии у рамы одной оси симметрии упругий центр будет лежать на этой оси и надо будет определить только одну его координату z_о.

Для рамы, имеющей две оси симметрии, упругий центр будет находиться на пересечении этих осей.

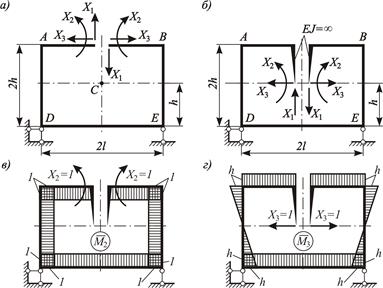
Рисунок 3.29 – Упрощение расчета рамы введением жестких консолей:

а – симметричная основная система; б – основная система с введенными жесткими консолями; в, г – единичные эпюры моментов

На рисунках 3.29, б-г приведены основная система, полученная с помощью введения абсолютно жестких консолей и перемещения неизвестных силовых факторов в упругий центр, а также единичные эпюры моментов 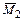и .

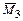Коэффициент 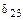, определяемый как результат перемножения этих эпюр, будет равен

,

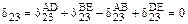где 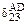, 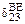– результат перемножения эпюр 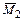и 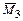соответственно на участках AD и BE;

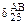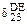, – то же на участках AB и DE.

Проанализируем результат перемножения эпюр по всем участкам рамы.

На участках AD и BE коэффициент 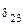будет равен нулю ( 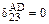и 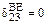), поскольку здесь перемножаются симметричные эпюры 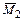и кососимметричные .

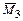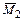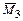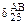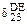На участках AB и DE эпюры и одинаковы по величине, но обратны по знаку. Соответственно в результате перемножения получаем и одинаковые по величине, но с разными знаками. При суммировании они дают нуль.

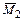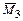Таким образом, в рассматриваемом случае эпюры и являются ортогональными.

Тогда канонические уравнения примут вид

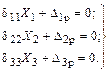
Таким образом, при переносе неизвестных в упругий центр обращается в нуль единственное оставшееся побочное перемещение 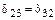и вместо системы уравнений получается 3 независимых уравнения.

Дата добавления: 2015-07-10