Выбор рациональной основной системы

При решении статически неопределимых систем с большим числом лишних неизвестных по возможности необходимо использовать те или иные методы, упрощающие расчет. Все существующие методы сводятся главным образом к упрощению составления и решения системы канонических уравнений. Основной метод упрощения расчета заключается в выборе рациональной основной системы.

Цель выбора рациональной основной системы – упрощение канонических уравнений и, следовательно, уменьшение трудоемкости расчетов.

Критерием рациональности основной системы является равенство нулю возможно большего числа побочных коэффициентов 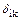, т.е.

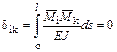. (3.23)

Эпюры 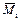и , удовлетворяющие условию (3.23), называются взаимно нулевыми или ортогональными (при перемножении дают нуль).

Примеры ортогональных эпюр:

одна из эпюр нулевая, а другая – прозвольной формы, отличная от нуля (рисунок 3.20, а);

симметричная и кососимметричная эпюры (рисунок 3.20, б).

Симметричные и кососимметричные эпюры при перемножении всегда дают нуль.

П р и м е ч а н и е – Это правило вытекает из того, что результат перемножения эпюр по левой половине рамы будет равен результату перемножения по правой половине с обратным знаком.

Рисунок 3.20 – Примеры ортогональных эпюр:

а – нулевая и произвольная эпюры; б – симметричная и кососимметричная эпюры

Если интеграл нельзя превратить в нуль, то желательно, чтобы эпюры занимали возможно меньший участок рамы и содержали возможно больше нулевых участков.

Упрощение расчета рассмотрим на примере стержневой системы, приведенной на рисунке 3.21, а. Возможные варианты основных систем для нее показаны на рисунках 3.21, б, в.

Рассматриваемая система имеет четыре замкнутых контура и поэтому 12 раз статически неопределима. Для раскрытия статической неопределимости произведем рассечением контуров.

В первом варианте основной системы рассечены вертикальные стержни, во втором – горизонтальные. В местах разреза необходимо ввести три внутренних силовых факторов. С целью наглядности, ограничимся рассмотрением только перерезывающих сил , , 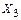и .

На рисунках 3.21, г, д показаны эпюры моментов от единичных силовых факторов и для обоих вариантов основной системы.

Первый вариант характеризуется тем, что эпюры моментов от усилия занимают всю длину рамы, от единичных усили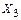й , и – часть рамы. В результате все побочные коэффициенты системы .

Во втором варианте построение эпюр от каждого единичного силового фактора замыкается на одном контуре, которому принадлежит данное неизвестное. На остальных контурах имеют место нулевые участки эпюр. При использовании данного варианта 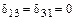и . Следовательно, второй вариант основной системы является более рациональным.

Рисунок 3.21 – К выбору рациональной основной системы:

а – исходная система; б, в – варианты основных систем; г, д – эпюры и соответственно для первого и второго вариантов основных систем

Дата добавления: 2015-07-10