Построение окончательных эпюр внутренних сил для заданной системы

Заключительным этапом расчета статически неопределимых систем является построение эпюр внутренних усилий.

Ординаты окончательных (суммарных) эпюр 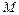, 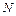и 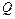получают в результате суммирования по характерным точкам ординат эпюр от внутренних сил , …, и от внешней нагрузки

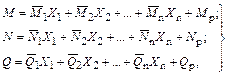(3.18)

где 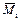, – соответственно ординаты эпюр изгибающих моментов в рассматриваемом сечении основной системы от Х _i = l и внешней нагрузки;

, – то же ординаты эпюр продольных сил;

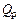, – то же ординаты эпюр поперечных сил.

Построение окончательной эпюры моментов. В первую очередь строят окончательную эпюру изгибающих моментов М, используя первое уравнение формулы (3.18).

Практически построение окончательной эпюры 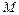производится следующим образом:

· ординаты единичных эпюр увеличиваются в раз;

· полученные ординаты алгебраически суммируются с ординатами грузовой эпюры для узловых и характерных точек рамы.

П р и м е ч а н и е – При построении эпюр рекомендуются нумеровать узлы и характерные точки рамы

Результирующая эпюра изгибающих моментов 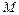является основной для проверки прочности рам. Она может использоваться также для построения эпюр поперечных и продольных сил.

Поэтому обычно производится контроль правильности построения окончательной эпюры изгибающих моментов М: статическая и кинематическая.

Статическая проверка является вспомогательной и заключается в проверке равновесия узлов рамы.

Алгебраическая сумма ординат эпюры моментов в любом узле рамы должна быть равна нулю, т. е. должно соблюдаться условие .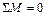

Кинематическая (деформационная) проверка заключается в перемножения окончательной М и суммарной единичной эпюр. Результат перемножения должен быть равен нулю.

Это условие в общем виде имеет вид

. (3.19)

Допускается невязка не более 5%.

Так же, как и при проверке коэффициентов канонических уравнений вместо универсальной проверки по формуле (3.19) можно выполнять построчную проверку

. . (3.20)

Отметим, что кинематическая проверка достаточна, если все эпюры изгибающих моментов в основной системе построены правильно.

Совокупность статической и кинематической проверок является достаточной во всех случаях.

Построение окончательных эпюр поперечных и продольных сил. Для построения эпюры поперечных сил Q можно воспользоваться третьим уравнением формулы (3.18). Однако, в практических расчетах эпюру поперечных сил Q более удобно строить непосредственно по окончательной эпюре моментов M.

Эпюры поперечных сил в этом случае строят для каждого элемента рамы в отдельности.

Для определения поперечной силы на тех участках рамы, где эпюра моментов имеет прямолинейное очертание, используется дифференциальная зависимость между нею и изгибающим моментом

, (3.21)

где – угол наклона линии, ограничивающей эпюру моментов, к оси элемента (рисунок 3.17).

Для эпюр моментов, приведенных на рисунке 3.17, значения поперечной силы в соответствии с формулой (3.21) будут равны:

(рисунок 3.17, а);

(рисунок 3.17, б);

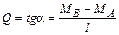(рисунок 3.17, в).

Эпюра поперечных сил в этом случае будет постоянной на всей длине элемента рамы.

Если эпюра имеет ломаное очертание, ее разбивают на участки с прямолинейным очертанием (рисунок 3.17, г). Тогда

, .

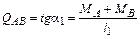Введем правило знаков для поперечной силы. Поперечную силу считают положительной, если для совмещения оси элемента с линией, ограничивающей эпюру изгибающих моментов, или с касательной к эпюре М приходится эту ось поворачивать по часовой стрелке (в сторону меньшего угла).

Рисунок 3.17 – К построению эпюры поперечных сил по эпюре изгибающих моментов: а, б, в – для линейных эпюр моментов; г – для эпюры моментов с ломаным очертанием

Поперечную силу можно также определять, рассматривая каждый из элементов рамы как шарнирно опертую по концам статически определимую балку, нагруженную соответствующей внешней нагрузкой (Р или q) и узловыми моментами и (рисунок 3.18). Узловые моменты возмещают жесткость прикрепления концов балки к узлам.

Рисунок 3.18 – К определению поперечной силы:

а – ненагруженная балка; б, в – нагруженная балка

Тогда, поперечная сила в сечении с абсциссой х:

, (3.22)

где – поперечная сила в сечении х однопролетной балки, вызываемая только внешней нагрузкой;

– изгибающие моменты в начале балки (при х = 0) и в конце (при х = l), взятые со своими знаками;

l – длина балки.

П р и м е ч а н и я

1 Второе слагаемое в формуле (3.22) представляет собой поперечную силу в сечениях балки от узловых моментов.

2 Как известно, момент считается положительным, если вызывает растяжение нижних волокон.

Формулу (3.22) обычно используют в тех случаях, когда на стержне или участке стержня эпюра моментов имеет криволинейное очертание, т.е. для элементов рамы, нагруженных равномерно распределенной нагрузкой.

Так, для балки с равномерно распределенной нагрузкой (рисунок 3.18, в) возможные эпюры моментов и соответствующие им эпюры поперечных сил показаны на рисунке 3.19. Узловые моменты на эпюрах имеют отрицательное значение.

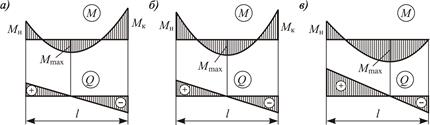
Рисунок 3.19 – К построению эпюры поперечных сил по эпюре моментов

с криволинейным очертанием:

а – для ; б – для 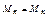; в – для

Поперечная сила в этом случае изменяется по линейному закону и будет иметь следующие значения:

в сечении с абсциссой х = 0

;

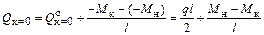в сечении с абсциссой х = l

,

где ; , .

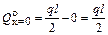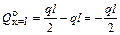Для построения эпюры продольных сил N можно воспользоваться вторым уравнением формулы (3.18) или построенной окончательной эпюрой поперечных сил Q. При этом в последнем случае применяют способ вырезания узлов рамы.

Сущность способа заключается в следующем. К каждому вырезанному узлу прикладывают действующую на него нагрузку, включая продольные и ранее найденные поперечные силы, и затем составляют для рассматриваемого узла уравнения равновесия. Полученные уравнения равновесия используют для определения искомых продольных сил.

П р и м е ч а н и е – Построение эпюры N следует начинать с определения продольных сил в одном из узлов, где сходятся не более двух элементов.

Проверка эпюр Q и N состоит в том, что для любой отсеченной части рамы сумма проекций на две оси всех действующих сил – внешних и внутренних – должна быть равна нулю.

Дата добавления: 2015-07-10