Анализ геометрической неизменяемости стержневых систем

Понятие о геометрической неизменяемости и степени свободы системы. Геометрическая неизменяемость системы характеризуется неизменяемостью ее форм и неподвижностью относительно основания. Изменение форм системы возможно лишь за счет деформации элементов. В частности, стержневая система является геометрически неизменяемой, если перемещения ее точек невозможны без изменения длин стержней.

Реальные конструкции должны быть геометрически неизменяемыми системами.

Установить, является ли рассматриваемая система геометрически неизменяемой, позволяет кинематический анализ, который должен предшествовать расчету системы.

Расчетные схемы конструкций могут быть представлены в виде системы геометрически неизменяемых тел (дисков), соединенных между собой и с основанием связями.

Роль диска может выполнять геометрически неизменяемая система (геометрически неизменяемая часть конструкции). В стержневой системе простейшим диском является стержень – прямолинейный или произвольной конфигурации. Землю (основание конструкции) также можно считать диском.

Кинематический анализ системы – проверка геометрической неизменяемости системы – включает два этапа:

1) определение степени свободы системы;

2) анализ структуры системы и условий опорных закреплений.

Таким образом, кинематический анализ системы начинают с установления степени ее свободы.

Рассмотрим определение степени свободы диска.

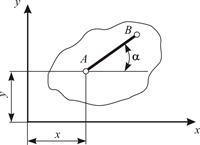
Как известно, положение отдельного диска на плоскости (рисунок 2.4) определяется тремя независимыми параметрами: координатами х и у произвольной точки А и углом наклона прямой АВ, проходящей через эту точку.

Количество независимых геометрических параметров, определяющих положение диска в плоскости или пространстве, называют числом степеней свободы диска.

Отсюда следует, что плоский диск имеет три степени свободы: два линейных и одно угловое перемещения.

Кинематические связи. Степень свободы диска или системы дисков можно ограничить путем введения различных устройств.

 

Рисунок 2.4 – Положение диска на плоскости

Устройство, устраняющее одну степень свободы, рассматривается как единичная кинематическая связь.

Связь, препятствующая взаимному перемещению двух дисков в одном определенном направлении, называют элементарной. Различают два вида элементарных связей: линейные – связи, препятствующие линейным перемещениям дисков, и угловые – препятствующие угловым перемещениям.

Связи, соединяющие диск (систему) с основанием называют опорными (внешними), а соединяющие элементы системы между собой – внутренними.

В качестве кинематических связей используют шарниры, соединительные стержни и опорные стержни (опоры).

Шарниры используются для соединения дисков и бывают простыми (рисунок 2.5, а) и сложными или кратными (рисунок 2.5, б). Простой шарнир соединяет два диска (стержня), сложный – более двух.

Рисунок 2.5 – Шарнирное соединение дисков (стержней):

а – простой шарнир; б – кратный шарнир

Каждый простой шарнир эквивалентен наложению двух кинематических связей, поскольку препятствует любым двум взаимным смещениям двух дисков (устраняет две степени свободы), оставляя возможность взаимного их поворота. Сложный (кратный) шарнир эквивалентен (n – 1) простым шарнирам, где n – число соединяемых дисков.

Стержень, оба конца которого шарнирно соединены с дисками, называют соединительным.

Различают следующие типы опор (опорных связей): цилиндрическая подвижная опора, цилиндрическая неподвижная опора и жесткая заделка.

Цилиндрическая подвижная опора (рисунок 2.6) эквивалентна наложению одной кинематической связи. Конструктивная схема опоры (рисунок 2.6, а) включает верхний и нижний балансиры, между которыми находится цилиндрический шарнир. Расчетную схему опоры (рисунок 2.6, б) принимают в виде стержня с шарнирами по концам. Опорный стержень устраняет одну степень свободы – линейное перемещение вдоль оси стержня и в нем возникает реакция R.

Рисунок 2.6 – Цилиндрическая подвижная опора: а – конструктивная схема; б – расчетная схема  

Цилиндрическая неподвижная опора (рисунок 2.7, а, б, в, г) эквивалентна двум кинематическим связям. Она препятствуют линейным перемещения системы в вертикальном и горизонтальном направлениях, т. е. устраняет две степени свободы Расчетную схему опоры принимают в виде двух опорных стержней, расположенных под углом друг к другу. В опоре возникает реакция V, проходящая через центр шарнира, направление которой зависит от направления расчетной нагрузки. При расчетах ее обычно заменяют двумя составляющими R и H, направленными по вертикали и горизонтали соответственно

Рисунок 2.7 – Цилиндрическая неподвижная опора:

а – конструктивная схема; б, в, г – расчетные схемы

Жесткая заделка (рисунок 2.8, а,б, в) – эквивалентна трем кинематическим связям. Она препятствует угловому (повороту) и двум линейным перемещениям (устраняет три степени свободы). В такой связи возникают три реакции R, H и М. Расчетная схема заделки может быть представлена тремя опорными стержнями (рисунок 2.8, в). Стержневой эквивалент заделки поясняет появление в ней опорного момента М. Введенным стержням соответствуют опорные реакции , , Н. Тогда , . Здесь а – глубина заделки.

Рисунок 2.8 – Жесткая заделка:

а – конструктивная схема; б, в – расчетные схемы

П р и м е ч а н и е – Обратите внимание на то, рассмотренные выше опорные связи удобно характеризовать числом опорных стержней. Так, цилиндрически неподвижная опора эквивалентна двум опорным стержням, заделка – трем опорным стержням. В свою очередь, каждый опорный стержень эквивалентен одной кинематической связи.

В строительной механике стержневых систем используют также связи, устраняющие одну степень свободы – угловые перемещения, которые становятся возможными в системе в результате выделения из стержневой симметричной системы ее части. Связи, показанные на рисунках 2.9, а, 2.9, б, и 2.9, в устраняют повороты концевого сечения стержня соответственно в плоскостях хОz (относительно оси Оу), хОу (относительно оси Оz) и уОz (относительно оси Ох).

Рисунок 2.9 – Связи, устраняющие угловые перемещения:

а – в плоскости xOz; б – в плоскости xOy; в – в плоскости yOz

Степень свободы плоской стержневой системы. Диски, образующие систему, соединяются между собой шарнирами и стержнями и прикрепляются к земле с помощью опорных стержней (опор).

Степень свободы системы (степень геометрической изменяемости системы), состоящей из нескольких дисков, может быть определена по формуле

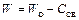, (2.1)

где – степень свободы системы без учета связей, ;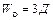

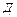– количество дисков;

– число связей, наложенных на систему,

;

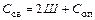Ш – число простых шарниров, связывающих диски;

– число опорных стержней.

П р и м е ч а н и е – Для определения числа дисков Д, входящих в систему, необходимо предварительно отбросить все шарниры и опоры, для определения числа шарниров Ш – все опорные стержни.

Тогда

. (2.2)

П р и м е ч а н и е – В формуле (2.2) учитывается, что:

· каждый диск имеет три степени свободы;

· каждый простой шарнир эквивалентен двум кинематическим связям (препятствует двум взаимным линейным смещениям соединяемых стержней, оставляя возможность взаимного их поворота);

· каждый опорный стержень эквивалентен одной линейной связи

По результатам определения степени свободы системы по формуле (2.2) могут быть сделаны следующие заключения о расчетной схеме конструкции:

1) если , то система является геометрически изменяемой, так как не имеет достаточного количества связей и по определению не может служить в качестве расчетной схемы конструкции. Система, для которой , называется механизмом;

2) если – система формально обладает необходимым минимумом связей, чтобы быть геометрически неизменяемой и статически определимой;

3) если – система имеет избыточные связи. В этом случае можно утверждать, что система является статически неопределимой. Однако ничего определенного нельзя утверждать относительно кинематической неизменяемости системы.

Пример 1. Установить степень свободы системы (рамы), приведенной на рисунке 2.10, а.

Р е ш е н и е.

Устанавливаем, что система имеет три диска (стержни I, II, III), т.е Д = 3, и четыре шарнира, эквивалентных простым (Ш = 4). Для определения числа дисков отбрасываем все шарниры и опорные стержни (рисунок 2.10, б), для определения числа простых шарниров – все опорные стержни (рисунок 2.10, в). Цифры на последней схеме указывают кратность шарниров.

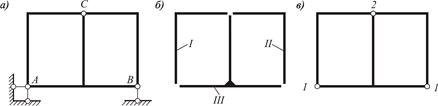
Рисунок 2.10 – К расчету степени свободы системы:

а – исходная система; б – схема для определения числа дисков; в – схема для определения числа простых шарниров

Число опорных стержней .

Тогда

.

Следовательно, система является статически неопределимой (имеет две лишние связи) и может быть геометрически неизменяемой.

Пример 2. Установить степень свободы систем в виде шарнирного треугольника (рисунок 2.11, а) и шарнирного прямоугольника (рисунок 2.11, б).

Р е ш е н и е.

Степень свободы рассматриваемых систем:

;

.

Следовательно, система в виде шарнирного треугольника обладает минимально необходимым числом связей (статически определима) и может быть геометрически неизменяемой.

Система в виде шарнирного прямоугольника представляет собой механизм, т.е. является геометрически изменяемой и не может быть использована в качестве конструкции.

Пример 3. Установить степень свободы системы, изображенной на рисунке 2.11, в.

Р е ш е н и е.

Для рассматриваемой двухопорной рамы Д = 2, Ш = 1, .

Рисунок 2.11 – К расчету степени свободы системы:

а – шарнирный треугольник; б – шарнирный прямоугольник; в – двухопорная рама

Степень свободы системы

.

Отсюда следует, что рассматриваемая система статически определима и может быть геометрически неизменяемой.

Степень свободы плоской шарнирно-стержневой системы. Шарнирно-стержневыми называют системы с шарнирными соединениями стержней. Степень свободы таких систем можно определить по формуле (2.2), как это мы делали для систем в виде шарнирных треугольника и прямоугольника. Однако для более сложных систем удобнее пользоваться другими.

Для шарнирно-стержневых систем выражения для и можно записать в виде:

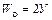, а ,

где – число узлов системы;

– число стержней системы;

– число опорных стержней.

П р и м е ч а н и е – В приведенных выражениях для и учитывается, что общее число степеней свободы всех узлов, не связанных между собой стержнями, равно 2 У (степень свободы шарнира (точки) равна двум), а каждый стержень системы (включая опорный) снимает у объединяемых им шарниров одну степень свободы, т.е. эквивалентен одной кинематической связи.

Тогда, степень свободы шарнирно-стержневой системы

. (2.3)

Пример. Установить степень свободы системы, изображенной на рисунках 2.12, а, б, в.

Р е ш е н и е.

Для рассматриваемых систем У = 10, , С = 13 – для первой системы, С = 17 – для второй, С = 21 – для третьей.

Степень свободы рассматриваемых систем:

первой – ;

второй – ;

третьей – .

Следовательно, первая шарнирно-стержневая система (рисунок 2.12, а) является геометрически изменяемой; вторая (рисунок 2.12, б) – статически определима и может быть геометрически неизменяемой; третья (рисунок 2.12, в) – статически неопределима, так как имеет избыточные связи.

Рисунок 2.12 – Шарнирно-стержневые системы:

а – геометрически изменяемая; б – статически определимая; в – статически неопределимая

Анализ геометрической структуры системы. Для неизменяемых систем должно соблюдаться условие 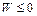, т.е. количество наложенных кинематических связей должно быть не менее степени свободы системы (без учета связей).

Аналитическое условие 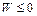является необходимым, но недостаточным для утверждения о неподвижности и геометрической неизменяемости системы.

Это связано с тем, что геометрическая неизменяемость системы зависит не только от числа связей, наложенных на диски, но и от их расположения.

Чтобы узнать, является ли система действительно геометрически неизменяемой и неподвижной проводят анализ геометрической структуры системы. Для этого в системе выделяют неизменяемые части (диски) и исследуют их соединение между собой.

Рассмотрим основные принципы образования структурно неизменяемых систем:

1) два диска (I и II) или диск с землей могут быть соединяться в неизменяемую систему (жестко) при помощи трех элементарных связей:

· либо шарниром С и стержнем АВ, ось которого не проходит через центр шарнира (рисунки 2.13, а, б);

· либо тремя стержнями, оси которых не пересекаются в одной точке и не параллельны (рисунки 2.13, в, г);

3) три диска (I, II и III)) могут быть соединены жестко тремя шарнирами, не лежащими на одной прямой (рисунок 2.13, д);

4) новый узел (В) может быть присоединен к диску при помощи диады – двух линейных связей (стержней), не лежащих на одной прямой (рисунок 2.13, е).

Все перечисленные способы могут быть сведены к шарнирно-стержневому треугольнику (рисунок 2.13, ж), который является геометрически неизменяемой фигурой.

Рисунок 2.13 – Образование плоских неизменяемых систем:

а, б – соединение двух дисков шарниром и стержнем; в, г – соединение двух дисков тремя стержнями; д – соединение трех дисков тремя шарнирами; е – присоединение нового узла к диску; ж – шарнирно-стержневой треугольник

Напомним, что в плоских стержневых системах простейшим диском является стержень, диском является и земля.

Примеры неподвижного прикрепления стержневых систем к земле (диску) с помощью шарнира А и стержня в соответствии с указанными правилами приведены на рисунке 2.14, а; тремя стержнями – рисунках 2.14, б, в, г.

При анализе стержневых систем на структурную неизменяемость их разбивают на диски, неизменяемость которых очевидна. В этом случае для анализа неизменяемости всей системы достаточно проанализировать соединение дисков между собой.

Пример 1. Выполнить анализ структуры системы, приведенной на рисунке 2.10, а.

Так как три диска (стержни I, II, III) соединены тремя шарнирами А, В и С, не лежащими на одной прямой, они образуют единый жесткий диск. В свою очередь, этот диск присоединен к основанию (земле) тремя опорными стержнями, не пересекающимися в одной точке.

Следовательно, система является неизменяемой, поскольку она образована в полном соответствии с основными принципами образования структурно неизменяемых систем.

Рисунок 2.14 – Примеры неподвижного прикрепления стержневых систем к земле

Пример 2. Произвести анализ геометрической структуры шарнирно-стержневой системы, показанной на рисунке 2.11, а.

Аналогично предыдущему примеру три диска – стержня (I, II, III) соединены тремя шарнирами, не лежащими на одной прямой и их можно рассматривать, как единый диск. Полученный диск связан неподвижно с землей с помощью трех опорных стержней, которые не пересекаются в одной точке. Таким образом, рассматриваемая система, является неизменяемой.

Шарнирный треугольник является примером простейшей геометрически неизменяемой стержневой системой.

Пример 3. Исследуем систему, приведенную на рисунке 2.11, в.

Диск I жестко присоединен к земле заделкой (тремя стержнями, не пересекающимися в одной точке). Диск II соединен с диском I, а, следовательно, с землей, шарниром С и стержнем (ось стержня не пересекает ось шарнира). Следовательно, диски I и II можно объединить в единый блок, который неподвижно связан с землей. Таким образом, система на рисунке 2.11, в является геометрически неизменяемой.

Пример 4. Выполнить анализ структуры системы, приведенной на рисунке 2.12, б.

Анализ структуры рассматриваемой системы показывает, что она состоит из последовательно присоединенных шарнирных треугольников, т.е. представляет собой единый блок. Система неподвижно присоединена к земле тремя стержнями.

Отсюда следует, что данная система геометрически неизменяема.

Таким образом, последовательность проверки геометрической неизменяемости системы следующая.

1 В системе выделяют диски – геометрически неизменяемые части, и устанавливают число наложенных на систему связей: шарниров и опорных стержней.

2 Определяют степень свободы системы 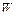, используя формулы (2.2) или (2.3).

3 В случае выполнения условия 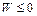проверяют еще геометрическую структуру системы, выделяя возможно более крупные геометрически неизменяемые части (диски) системы и исследуя их соединение между собой.

4 На основании расчета 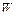и анализа геометрической структуры могут быть сделаны следующие заключения о расчетной схеме системы:

· если и все соединения элементов допустимы, система является геометрически неизменяемой и статически определимой;

· если и все соединения элементов допустимы, система является геометрически неизменяемой и статически неопределимой.

Мгновенно изменяемые системы. Все исключения из принципов образования геометрически неизменяемых систем приводят к мгновенно изменяемым системам.

Мгновенно изменяемой называют систему, точки которой получают конечные перемещения даже при бесконечно малых деформациях элементов. Поэтому такие системы неприменимы в качестве инженерных конструкций.

Геометрические признаки мгновенно изменяемых систем:

1) шарнир А находится на одной прямой со стержнем 1 (рисунок 2.15, а);

2) шарниры А, В и С лежат на одной прямой (рисунок 2.15, б);

3) стержни 1, 2 и 3 параллельны или пересекаются в одной точке (рисунок 2.15, в).

Рисунок 2.15 – Примеры плоских мгновенно изменяемых систем

Дата добавления: 2015-07-10