|
Читайте также: |
При расчете многопролетных симметричных рам не всегда удается разместить все неизвестные в сечениях по оси симметрии.
В этом случае для получения симметричных и кососимметричных эпюр целесообразно принимать групповые неизвестные, расположив их в различных симметрично расположенных точках.
Проиллюстрируем данный способ для двухпролетной рамы, приведенной на рисунке 3.27, а.
При традиционном способе решения основная система и единичные эпюры показаны на рисунках 3.27, б–г.
При использовании традиционного способа все побочные коэффициенты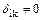 
.
При использовании способа группировки неизвестных упрощение расчета обеспечивается тем, что в качестве лишних неизвестных принимают не отдельные силы, а группы сил.
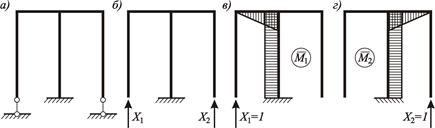
Рисунок 3.27 – Традиционный способ решения системы:
а – исходная система; б – основная система; в, г – единичные эпюры моментов
П р и м е ч а н и е – Групповые неизвестные подбирают так, чтобы получающиеся от их действия эпюры были ортогональными (симметричными и кососимметричными).
Для рамы, изображенной на рисунке 3.27, а, реакции удаленных связей, которые обозначим как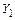 
и 
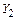, заменим эквивалентными им новыми неизвестными – парами симметричных 
и кососимметричных 
сил. Реакцию левой опоры 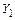представим суммой сил и , а реакция правой опоры 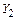– разностью этих сил (рисунок 3.28, а), т.е.
; 
.
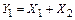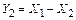П р и м е ч а н и е – Неизвестное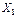 
представляет собой две симметрично расположенные силы, а 
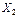– две кососимметричные силы.
Эпюры моментов от единичных групповых силовых факторов показаны на рисунках 3.28, б, в.
В результате перемножения эпюр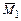 
и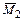 
получаем 
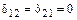. Это следует также из правила 1.
В результате получаем канонические уравнения с полностью разделенными неизвестными, каждое из которых содержит только по одному лишнему неизвестному
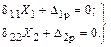
Использование групповых неизвестных значительно упрощает расчет симметричных рам с большим числом лишних неизвестных.
П р и м е ч а н и е – Сущность способа группировки неизвестных состоит в том, что в качестве неизвестных принимают не отдельные силы, а группы сил, составленные так, чтобы получающиеся от их действия эпюры были ортогональными.
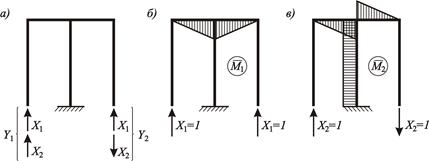
Рисунок 3.28 – Упрощение расчета рамы с помощью способа группировки
неизвестных:
а – основная система; б, в – единичные эпюры моментов
Дата добавления: 2015-07-10; просмотров: 222 | Нарушение авторских прав