|
Читайте также: |
Рассмотрим особенности расчета рамы вагона-платформы.
Расчетная схема. Для расчета используем расчетную схему, которая показана на рисунке 3.41, а. Ее обоснование приведено в п. 1.2. Рама загружена внешней продольной сжимающей силой, которая передается на хребтовую балку рамы через задние упоры автосцепного устройства. Рассматриваемая расчетная схема является плоской стержневой.
Степень статической неопределимости системы. Степень статической неопределимости расчетной схемы рамы платформы равна десяти.
Симметричность конструкции и загружения рамы относительно двух осей позволяет упростить расчет, рассматривая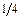 
часть рамы (рисунок 3.41, б). Действие отброшенной части заменяем введением связей от ненулевых силовых факторов: от продольной силы N – при разрезе продольных балок, от изгибающего момента М – при разрезе поперечных балок.
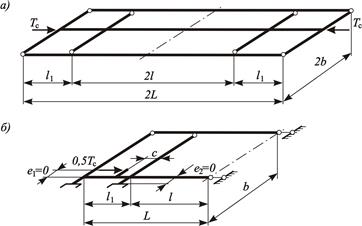
Рисунок 3.41 – Расчетная схема рамы платформы:
а – всей конструкции; б – ¼ части рамы
Поскольку хребтовая балка рассекается вдоль продольной оси пополам, в расчетной схеме 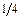части рамы она загружается продольной силой 
.
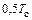Степень статической неопределимости 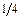части рамы снижается до двух, что значительно упрощает расчет.
Выбор основной системы. Основную систему получаем из заданной путем отбрасывания лишних связей – рассекая шарниры в местах соединения поперечных балок с продольной – и введения в местах разреза лишних неизвестных.
Основная система при традиционном способе решения имеет вид, показанный на рисунке 3.42, а. Здесь неизвестные усилия обозначены как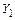 
и 
.
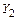Однако, более удобным будет вариант основной системы при использовании способа группировки неизвестных. Групповые незвестные 
и 
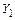показаны на рисунках 3.42, б, в. Суммируя групповые неизвестные и путем наложения схем, приведенных на рисунках 3.43, б, в, мы должны получить исходные неизвестные и 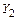. Групповые неизвестные и связаны с исходнымии неизвестными следующими зависимостям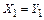и: 
и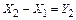 
.
Полученный рациональныий вариант основной системы показан на рисунке 3.42, г.
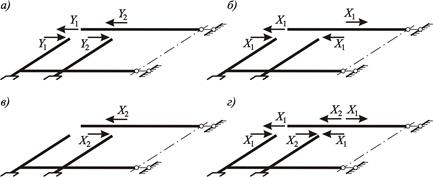
Рисунок 3.42 – К выбору основной системы:
а – традиционная; б, в – основная система, загруженная групповыми неизвестным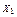и 
и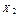 
; г – рациональная основная система
Составление канонических уравнений. Канонические уравнения для двух лишних неизвестных имеет вид:
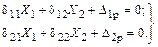
Определение коэффициентов и свободных членов канонических уравнений. Коэффициенты 
и свободные члены 
вычисляем по формулам перемножения эпюр с учетом деформаций изгиба и растяжения-сжатия
;
.
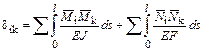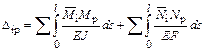Единичные и грузовые эпюры изгибающих моментов (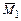
, 
, 
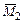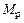) и продольных сил (
, 
, 
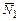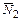) показаны на рисунках 3.43, а, б, в.
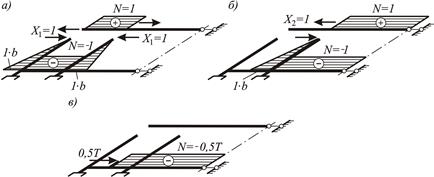
Рисунок 3.43 – Эпюры изгибающих моментов и продольных сил:
а – от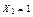 
; б – от 
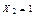; в – от внешней нагрузки
Решение канонических уравнений. Решая канонические уравнения, находим значения неизвестных и .
Построение окончательной эпюры моментов и продольных сил для заданной системы. Ординаты окончательной эпюры изгибающих моментов и продольных сил определяем по формулам:
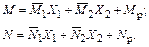
Значения ординат этих эпюр используются для оценки прочности рамы платформы.
Дата добавления: 2015-07-10; просмотров: 468 | Нарушение авторских прав