Составление канонических уравнений

Канонические уравнения метода перемещений (уравнения равновесия) характеризуют статическую эквивалентность основной и заданной систем

(4.2)

где 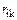– коэффициент канонического уравнения метода перемещений (реакция в i -й связи от смещения k -й связи на величину =1);

– свободный член канонического уравнения метода перемещений (реакция в i -й связи от действия внешней нагрузки);

– неизвестное перемещение i -й связи.

Примечание – Число уравнений равно числу введенных связей, т.е. степени кинематической неопределимости системы.

Каждое из уравнений выражает собой равенство нулю реакции во введенной связи от действия нагрузки и основных неизвестных. В частности, смысл первого уравнения – это отрицание реакции во введенной первой связи, второго уравнения – во второй связи и т.д.

Таким образом, в основе уравнений метода перемещений лежит отрицание реакций (реактивных усилий) по направлениям неизвестных перемещений.

В матричной форме система канонических уравнений имеет вид

,

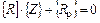Где 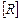– матрица реакций (коэффициентов канонических уравнений);

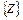– матрица-столбец неизвестных перемещений узлов;

– матрица-столбец грузовых реакций (свободных членов канонических уравнений).

Дата добавления: 2015-07-10