Выбор основной системы. Основная система метода перемещений должна быть кинематически определимой

Основная система метода перемещений должна быть кинематически определимой. Чтобы выполнить это требование узлы рамы закрепляют от поворотов и линейных смещений введением дополнительных связей.

Основную систему получают из заданной (см. рисунок 4.1):

1) введением дополнительных (фиктивных) связей, устраняющих угловые и линейные перемещения узлов (рисунок 4.6, а);

2) заданием введенным связям соответствующих угловых и линейных перемещений (рисунок 4.6, б).

П р и м е ч а н и е – Общее число введенных в основную систему связей равно, естественно, числу неизвестных метода перемещений.

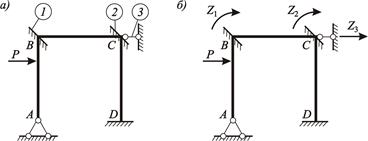
Рисунок 4.6 – К выбору основной системы метода перемещений:

а – рама с введенными дополнительными связями; б – основная система

В качестве дополнительных вводятся следующие связи:

угловая связь («плавающая заделка») – вводится во все жесткие узлы для устранения их поворотов (угловых перемещений);

линейная связь – вводится в необходимые места заданной системы для устранения линейных перемещений узлов (об этом информирует шарнирная система).

В рассматриваемом случае две угловые связи («плавающие заделки») с номерами 1 и 2 вводятся для устранения поворота жестких узлов В и С, линейная связь (номер 3) – для устранения линейных перемещений этих же узлов.

П р и м е ч а н и е – Заделка называется «плавающей», поскольку такая связь оказывает препятствие лишь повороту узла, но не лишает его линейной подвижности.

Кинематическая эквивалентность основной и заданной систем достигается тем, что связям одновременно с их введением задают соответствующие угловые и линейные перемещения .

На рисунке 4.6 через , и обозначены заданные перемещения введенных связей (показаны стрелками на основной системе).

П р и м е ч а н и е:

1 Заданные перемещения 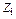введенных связей имеют такой же индекс, как и номер фиктивной связи. В рассматриваемом случае 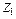, 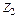– угловые перемещения узлов В и С, устраняемые заделками 1 и 2; 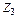– линейное перемещение узлов В и С, устраняемое стержнем 3.

2 Углы поворота введенных связей (в нашем случае 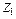и 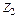) условно задаются по часовой стрелке, линейные перемещения (в нашем случае 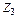) – слева – направо.

   

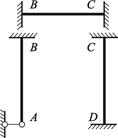
Рисунок 4.7 – Представление основной системы совокупностью статически неопределимых балок

Таким образом, расчету подлежит не заданная система, а преобразованная (основная) система, которая должна быть эквивалентна ей в статическом и кинематическом отношениях.

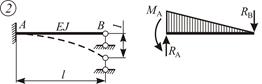
Введенные связи расчленяют получаемую основную систему на отдельные простейшие статически неопределимые балки – конечные элементы (рисунок 4.7). Каждая из этих балок хорошо изучена и результаты их расчета на стандартные воздействия приводятся в справочных данных (таблица 4.1).

Таблица 4.1 – Результаты расчета эпюр изгибающих моментов однопролетных статически неопределимых балок

Схема балки и воздействия на нее	Эпюры изгибающих моментов и реакции	Формулы
	;
	;
	; ; ;
	; ; ;
	; ; ; ;

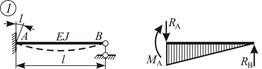
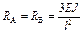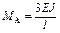
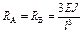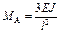
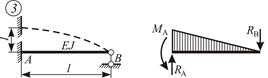
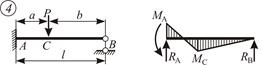
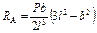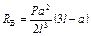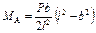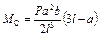
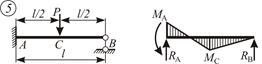
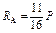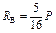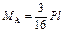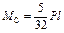
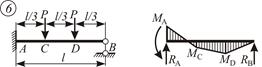
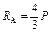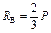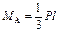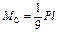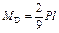
Продолжение таблицы 4.1

Схема балки и воздействия на нее	Эпюры изгибающих моментов и реакции	Формулы
	; ; ; ;
	; ; ;
	; ;
	;
	; ; ; ;
	;

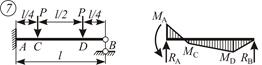
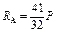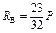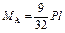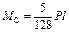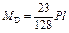
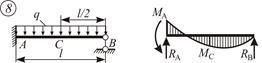
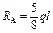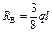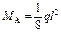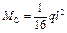
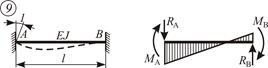
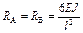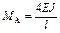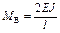
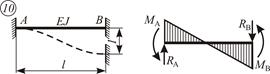
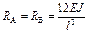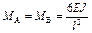
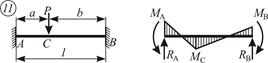
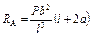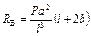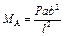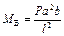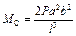
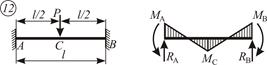
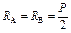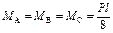
Окончание таблицы 4.1

Схема балки и воздействия на нее	Эпюры изгибающих моментов и реакции	Формулы
	; ;
	; ;
	; ;

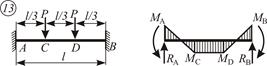
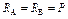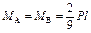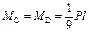
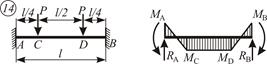
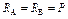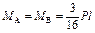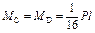
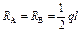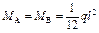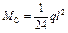
П р и м е ч а н и я

1 Таким образом, основная система метода перемещений представляет собой совокупность независимых элементов – однопролетных статически неопределимых балок, изображенных на рисунке 4.7. В рассматриваемом случае балки ВС и СD – балки с защемлениями по концам, АВ – балка с защемлением и шаровой опорой.

2 В отличие от метода сил, основная система метода перемещений является единственной

Дата добавления: 2015-07-10