Установление степени кинематической неопределимости

Приступая к расчету, прежде всего, необходимо определить число неизвестных – независимых угловых и линейных перемещений узлов рамы. Каждый узел рамы от нагрузки (либо других воздействий) может получить угловое и линейное перемещение.

Общее число неизвестных перемещений (степень кинематической неопределимости)

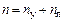, (4.1)

где – число угловых перемещений узлов (степень угловой подвижности узлов);

– число линейных перемещений узлов (степень линейной подвижности узлов).

Рассмотрим определение перемещений и для заданной системы (рисунок 4.1).

Число угловых перемещений узлов равно числу жестких узлов рамы. Опорные узлы при этом не учитываются.

Примеры жестких (комбинированных) узлов показаны на рисунке 4.2.

Заданная система имеет 4 узла: A, D – опорные узлы; B, C – жесткие узлы.

Тогда

.

П р и м е ч а н и е – Таким образом, определение сводится к простому подсчету числа жестких и комбинированных (жесткошарнирных) узлов системы.

Рисунок 4.1 – Расчетная схема рамы	Рисунок 4.2 – Примеры узлов рамы: а – жестких; б – комбинированных

Число линейных перемещений узлов равно числу стержней, которые необходимо ввести в шарнирную схему конструкции для превращения ее в геометрически неизменяемую систему.

П р и м е ч а н и е – Определение для рам базируется на следующих допущениях, принятых в методе перемещений:

учитываются лишь деформации изгиба (влиянием продольных и поперечных сил на перемещение узлов пренебрегают);

расстояние между узлами при изгибе прямых стержней не меняются;

угол между стержнями при деформации не меняется (концы стержней, соединенных жестко в узле, поворачиваются на один и тот же угол);

углы поворота вследствие малых значений принимаются равными их тангенсам.

Последовательность определения :

1) заданную систему заменяют ее шарнирной схемой, поставив шарниры во все узлы, включая опорные (рисунок 4.3, а);

2) полученную шарнирную схему превращают в геометрически неизменяемую систему путем постановки дополнительных стержней (рисунок 4.3, б).

Поясним, как установить количество вводимых стержней.

Число степеней свободы полученной шарнирной схемы, определяемое по формуле (2.2), равно числу линейных перемещений узлов рамы .

Для рассматриваемого случая . Для устранения этого перемещения достаточно поставить дополнительный опорный стержень (см. рисунок 4.3, б).

Можно также определять по смыслу, не используя формулу (2.2), последовательно закрепляя узлы шарнирной схемы от линейных смещений.

На рисунке 4.3, а введены следующие обозначения:

штриховая линия – возможные перемещения сторон полученной шарнирной схемы;

, – линейные перемещения узлов В и С, причем .

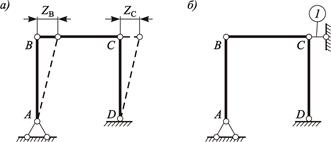
Рисунок 4.3 – К последовательности определения числа линейных перемещений узлов рамы:

а – шарнирная схема; б – геометрически неизменяемая система

На рисунке 4.3, б цифрой 1 обозначена введенная линейная связь в виде стержня продольного направления.

П р и м е ч а н и е – Шарнирная схема рассматриваемой рамы один раз геометрически изменяема, так как для превращения ее в геометрически неизменяемую систему необходимо ввести один стержень. После включения этого стержня узел С будет прикреплен к земле с помощью двух стержней, оси которых не лежат на одной прямой. Следовательно, узел С будет геометрически неизменяемо связан с землей.

Поскольку мы ввели одну линейную связь, то .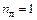

Тогда, общее число неизвестных перемещений .

 

Рисунок 4.4 – Деформированное состояние рамы  

Отсюда следует, что деформированное состояние рамы будет определено тремя перемещения узлов: , и . Причем , – угловые перемещения узлов В и С; – линейное перемещение стержня ВС (узлов В и С).

Деформированное состояние рамы показано на рисунке 4.4. Оно характеризуется тем, что упругие линии деформированных стержней рамы будут изгибаться под действием внешней нагрузки. В узлах В и С касательные к упругой линии стержня ВС повернутся соответственно на угол и , который называется углом поворота узла. Узлы В и С получат также смещение по горизонтали на .

Рассмотрим теперь раму, изображенную на рисунке 4.5, а. Число ее жестких узлов равно двум, следовательно, . Шарнирная схема рамы дважды геометрически изменяема (). Поэтому для превращения ее в геометрически неизменяемую необходимо ввести два стержня 1 и 2 (рисунок 4.5, б). Общее число неизвестных в рассматриваемой системе .

Рисунок 4.5 – К определению числа неизвестных перемещений рамы

Дата добавления: 2015-07-10