
Читайте также:
|
Если множество рациональных чисел объединить с множеством иррациональных чисел, то получится множество действительных чисел. Множество действительных чисел обычно означают буквой 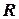 ; используют также символическую запись
; используют также символическую запись 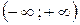 .
.
Действительные числа изображают точками координатной прямой (числовой оси).
Определение 1.8. Координатная прямая – это всякая прямая, на которой выбраны направление, принимаемое за положительное, точка – начало отсчета и единица измерения – масштабный отрезок, длина которого принимается равной единице.
Пусть  и
и  - действительные числа и
- действительные числа и 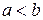 . В таблице 1.1 даны названия, определения и обозначения числовых множеств, называемых числовыми промежутками, и их изображение на координатной прямой. Каждый из числовых промежутков определяется как множество действительных чисел
. В таблице 1.1 даны названия, определения и обозначения числовых множеств, называемых числовыми промежутками, и их изображение на координатной прямой. Каждый из числовых промежутков определяется как множество действительных чисел  , удовлетворяющих определенным неравенствам.
, удовлетворяющих определенным неравенствам.
Таблица 1.1
| Название | Неравенство, определяющее множество | Обозначение | Изображение |
отрезок от 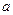 до до 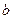 (замкнутый промежуток) (замкнутый промежуток)
| 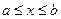
| 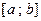
|
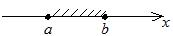
|
интервал от 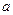 до до 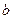 (открытый промежуток) (открытый промежуток)
| 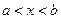
| 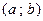
|
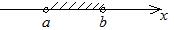
|
открытый слева промежуток от 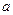 до до 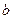
| 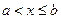
| 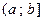
|
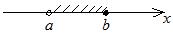
|
открытый справа промежуток от 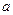 до до 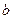
| 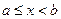
| 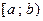
|
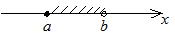
|
числовой луч от 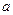 до до 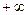
| 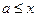
| 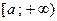
|
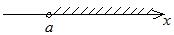
|
открытый числовой луч
от 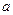 до до 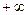
| 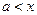
| 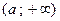
|

|
числовой луч
от 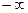 до до 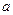
| 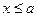
| 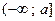
|
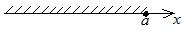
|
открытый числовой луч
от 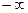 до до 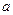
| 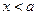
| 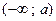
|
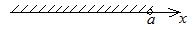
|
Дата добавления: 2015-07-10; просмотров: 150 | Нарушение авторских прав