Способы нахождения наибольшего общего делителя (НОД).

1) Разложить числа на простые множители и найти произведение общих простых множителей, взяв каждый из них с наименьшим (из имеющихся) показателем.

2) Выписать все общие делители чисел и выбрать из них наибольший.

3) Алгоритм Евклида: поэтапно заменять большее из двух имеющихся чисел на разность между ним и меньшим до тех пор, пока числа не станут равными.

Определение 1.5. Два натуральных числа - и - называют взаимно простыми числами, если у них нет общих делителей, отличных от 1, то есть НОД .

Теорема 1.3. Если даны натуральные числа и , причем - простое число, то либо делится на , либо и - взаимно простые числа.

Пример 1.4. Найти НОД (32, 76).

Решение. Разложим данные числа на простые множители: ; 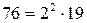. Следовательно, НОД (32, 76) .

Ответ: 4.

Пример 1.5. Найти НОД (945, 301).

Решение. Воспользуемся алгоритмом Евклида:

Следовательно, НОД (945, 301) .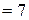

Ответ: 7.

Определение 1.6. Общим кратным натуральных чисел называется натуральное число, кратное каждому из них.

Определение 1.7. Наименьшим общим кратным (НОК) натуральных чисел называется наименьшее натуральное число, кратное этим числам.

Чтобы найти наименьшее общее кратное нескольких чисел, надо разложить эти числа на простые множители и найти произведение всех получившихся простых множителей, взяв каждый из них с наибольшим (из имеющихся) показателем.

Пример 1.6. Найти НОК(1044; 1512; 2436).

Решение. Разложим данные числа на множители:

; ; .

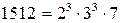Выпишем все множители одного из них, например, большего числа – 2436, и припишем к ним недостающие множители из разложений других чисел: . Перемножим их, получим число 43 848.

Ответ: 43 848.

Свойство 10. Если - общее кратное чисел и , то .

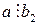Свойство 11. Если и , то .

Свойство 12. Если 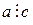и , то - общее кратное чисел и .

Пример 1.7. Доказать, что для любого натурального числа 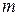справедливо соотношение .

Решение. В примере 1.1. было доказано, что многочлен делится на 2, 3, 4, 5, 8. Тогда по свойству 11 он делится и на НОК чисел 2, 3, 4, 5, 8, то есть на 120.

Теорема 1.4. Для любых натуральных чисел и справедливо равенство

.

(1.2)

Следствие 1.1. Если числа и взаимно простые, то .

Свойство 13. Если , 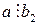и числа , - взаимно простые, то .

Свойство 14. Если и - взаимно простые числа и 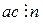, то .

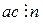Свойство 15. Если - простое число и , то хотя бы одно из чисел , 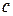делится на .

Пример 1.8. Произведение двух чисел равно 10 800, а их НОД равен 60. Найти НОК этих чисел.

Решение. Воспользуемся формулой (1.2). Из условия известно, что ; . Тогда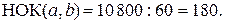

Ответ: 180.

Пример 1.9. Найти все пары натуральных чисел, НОД которых равен 5, а НОК равно 105.

Решение. По условию задачи, ; , где и - искомые числа. Так как числа имеют НОД, то каждое из них можно разложить на множители: 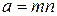; , где 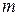, , 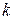- натуральные числа. Значит, ; . Получим систему условий

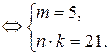
Число 21 имеет делители 1, 3, 7, 21. Его можно разложить на множители: ; . Тогда получим системы

или или или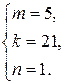

Из каждой системы имеем:

или или или

Таким образом, мы получили две пары чисел: (5; 105), (15; 35).

Ответ: (5; 105), (15; 35).

Дата добавления: 2015-07-10