Рациональные числа

Рациональные числа – это числа вида 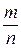, где 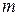- целое число, а - натуральное. Множество рациональных чисел обозначают буквой . При этом выполняется соотношение , так как любое целое число 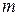можно представить в виде 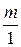. Таким образом, можно сказать, что рациональные числа – это все целые числа, а также положительные и отрицательные обыкновенные дроби.

Десятичные дроби – это такие обыкновенные дроби, у которых знаменатель – единица с нулями, то есть 10; 100; 1000 и т.д. Десятичные дроби записывают без знаменателей. Сначала пишется целая часть числа, справа от нее ставится запятая; первая цифра после запятой означает число десятых, вторая – сотых, третья – тысячных и т.д. Цифры, стоящие после запятой, называются десятичными знаками.

Бесконечной называется десятичная дробь, у которой после запятой бесконечно много цифр.

Каждое рациональное число 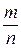может быть представлено в виде конечной или бесконечной десятичной дроби. Это достигается делением числителя на знаменатель.

Бесконечную десятичную дробь называют периодической, если у нее, начиная с некоторого места, одна цифра или группа цифр повторяется, непосредственно следуя одна за другой. Повторяющуюся цифру или группу цифр называют периодом и записывают в скобках. Например, .

Верно и обратное утверждение: любую бесконечную десятичную периодическую дробь можно представить в виде обыкновенной дроби.

Перечислим некоторые сведения о периодических дробях.

1. Если период дроби начинается сразу после запятой, то дробь называется чисто-периодической, если не сразу после запятой – смешанно-периодической.

Например, 1,(58) – чисто-периодическая дробь, а 2,4(67) – смешанно-периодическая.

2. Если несократимая дробь 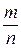такова, что в разложении ее знаменателя на простые множители содержатся лишь числа 2 и 5, то запись числа 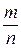в виде десятичной дроби представляет собой конечную десятичную дробь; если в указанном разложении есть другие простые множители, то получится бесконечная десятичная периодическая дробь.

3. Если несократимая дробь 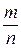такова, что в разложении ее знаменателя на простые множители не содержатся числа 2 и 5, то запись числа 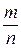в виде десятичной дроби представляет собой чисто-периодическую десятичную дробь; если в указанном разложении, наряду с другими простыми множителями, есть 2 или 5, то получится смешанно-периодическая десятичная дробь.

4. У периодической дроби период может быть любой длины, то есть содержать любое количество цифр.

Дата добавления: 2015-07-10