
|
Читайте также: |
Определение 2.6. Функция 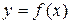 называется четной, если она обладает следующими двумя свойствами: 1) область определения этой функции симметрична относительно начала координат (то есть если точка
называется четной, если она обладает следующими двумя свойствами: 1) область определения этой функции симметрична относительно начала координат (то есть если точка  принадлежит области определения, то и точка
принадлежит области определения, то и точка 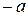 также принадлежит области определения); 2) для любого значения
также принадлежит области определения); 2) для любого значения  , принадлежащего области определения этой функции, выполняется равенство
, принадлежащего области определения этой функции, выполняется равенство  .
.
Определение 2.7. Функция 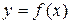 называется нечетной, если она обладает следующими двумя свойствами: 1) область определения этой функции симметрична относительно начала координат; 2) для любого значения
называется нечетной, если она обладает следующими двумя свойствами: 1) область определения этой функции симметрична относительно начала координат; 2) для любого значения  , принадлежащего области определения этой функции, выполняется равенство
, принадлежащего области определения этой функции, выполняется равенство 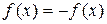 .
.
Замечание 2.1. График четной функции симметричен относительно оси ординат, а график нечетной функции симметричен относительно начала координат.

| 
| График четной функции 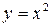 изображен на рисунке 2.4. График нечетной функции изображен на рисунке 2.4. График нечетной функции 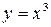 изображен на рисунке 2.5. Заметим, что не всякая функция является четной или нечетной.
Например, каждая из функций изображен на рисунке 2.5. Заметим, что не всякая функция является четной или нечетной.
Например, каждая из функций
 , ,  , , 
|
| рис. 2.4 | рис. 2.5 |
не является ни четной, ни нечетной. Такие функции называют функциями общего вида.
Дата добавления: 2015-07-10; просмотров: 83 | Нарушение авторских прав