
|
Читайте также: |
Изучение различных явлений связано с использованием переменных величин. Например, объем конуса зависит от радиуса его основания и высоты, цена покупки от веса товара, оценка на экзамене – от количества решенных задач и т. д.
Определение 2.1. Пусть заданы некоторые непустые числовые множества 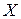 и
и 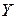 . Если каждому числу
. Если каждому числу  ставится в соответствие по некоторому закону
ставится в соответствие по некоторому закону  единственное значение
единственное значение  , то говорят, что на множестве
, то говорят, что на множестве 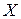 задана функция
задана функция 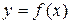 или
или  .
.
Переменную  называют независимой переменной (аргументом), а переменную
называют независимой переменной (аргументом), а переменную  - зависимой переменной (функцией от аргумента
- зависимой переменной (функцией от аргумента  ). Множество
). Множество 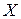 - областью определения функции, а множество всех значений
- областью определения функции, а множество всех значений  , таких, что
, таких, что 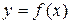 ,
,  , называют множеством значений (областью значений) функции.
, называют множеством значений (областью значений) функции.
Для функции  приняты обозначения:
приняты обозначения:  - область определения функции,
- область определения функции,  - множество значений функции,
- множество значений функции,  - значение функции в точке
- значение функции в точке  .
.
Если 
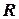 и
и 
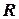 , то функцию называют числовой.
, то функцию называют числовой.
Элементы множества  также называют значениями аргумента, а соответствующие им элементы
также называют значениями аргумента, а соответствующие им элементы  - значениями функции.
- значениями функции.
Таким образом, символ 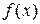 обозначает число
обозначает число  , которое в силу закона
, которое в силу закона  соответствует значению
соответствует значению  . Например,
. Например,  есть значение функции
есть значение функции  в точке
в точке  , если
, если  . Если же
. Если же  не принадлежит
не принадлежит 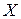 (
( ), то говорят, что функция
), то говорят, что функция  не определена в точке
не определена в точке  .
.
Существуют функции, для которых всем значениям  соответствует одно и то же значение
соответствует одно и то же значение  . В этом случае функции называют константами.
. В этом случае функции называют константами.
Если функция задана формулой и область определения не указана, то считают, что область определения состоит из всех значений независимой переменной, при которых эта формула имеет смысл. В этом случае говорят о естественной области определения функции.
Например, область определения функции  состоит из всех чисел, кроме числа
состоит из всех чисел, кроме числа 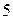 .
.
Пример 2.1. Найти область определения функции  .
.
Решение. Область определения данной функции задается условием
 .
.
Ответ:  .
.
Пример 2.2. Найти область определения функции  .
.
Решение. Учитывая, что для функции 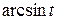 ,
,  , получаем область определения данной функции:
, получаем область определения данной функции:
 .
.
Ответ: 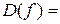
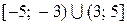 .
.
Пример 2.3. Найти область определения функции
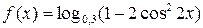 .
.
Решение. Область определения функции задается неравенством

 ,
, 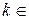
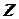

 ,
, 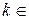
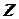 .
.
Ответ: 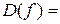
 ,
, 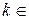
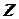 .
.
Пример 2.4. Найти множество значений функций
а)  ; б)
; б) 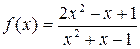 .
.
Решение. а)Преобразуем подкоренное выражение, выделив полный квадрат
 .
.
Учитывая ограниченность функции  :
:  , и, умножая, все части неравенства на положительное число
, и, умножая, все части неравенства на положительное число  , получаем
, получаем  . Вычтем из всех частей неравенства
. Вычтем из всех частей неравенства 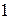 :
:  , тогда
, тогда  . Продолжим преобразования:
. Продолжим преобразования:



 .
.
б) Множество значений функции состоит из таких чисел  таких, для каждого из которых существует число
таких, для каждого из которых существует число  , являющееся решением уравнения
, являющееся решением уравнения 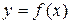 . Рассмотрим уравнение
. Рассмотрим уравнение 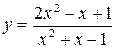 относительно неизвестной
относительно неизвестной  и выясним, при каких
и выясним, при каких  оно имеет решение:
оно имеет решение:
 .
.
При 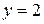 получаем линейное уравнение
получаем линейное уравнение  .
.
При  получаем квадратное уравнение, имеющее решение только в случае неотрицательного дискриминанта:
получаем квадратное уравнение, имеющее решение только в случае неотрицательного дискриминанта:


Ответ: а) 
 ; б)
; б) 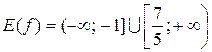 .
.
Пример 2.5. Найти множество значений функции
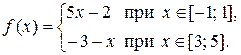
Решение. При  получаем
получаем  . При
. При  получаем
получаем 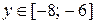 , тогда имеем
, тогда имеем 
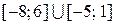 .
.
Ответ: 
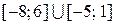 .
.
Определение 2.2. Функции 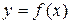 и
и 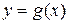 называются тождественно равными на множестве
называются тождественно равными на множестве 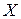 , если они определены на данном множестве и для каждого
, если они определены на данном множестве и для каждого  справедливо числовое равенство
справедливо числовое равенство  (при этом пишут
(при этом пишут  ).
).
Например: 1)  для всех
для всех 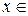
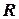 ; 2)
; 2)  ,
, 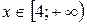 .
.
Определение 2.3 Графиком функции называется множество всех точек, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции.
Дата добавления: 2015-07-10; просмотров: 83 | Нарушение авторских прав