Монотонность функции

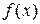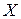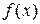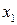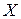Определение 2.4. Функция называется возрастающей на данном числовом промежутке , если большему значению аргумента соответствует большее значение функции , то есть для любых и из промежутка , таких, что , выполнено неравенство .

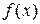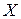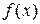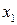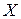Определение 2.5. Функция называется убывающей на данном числовом промежутке , если большему значению аргумента соответствует меньшее значение функции , то есть для любых и из промежутка , таких, что , выполнено неравенство .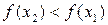

		Функция, только возрастающая или только убывающая на данном числовом промежутке, называется монотонной на этом промежутке. О монотонности функции можно судить по ее графику. Например, функция, график которой изображен на рисунке 2.2, возрастает при всех
рис. 2.2	рис. 2.3

значениях . Функция, график которой изображен на рисунке 2.3 убывает на и возрастает на промежутке .

Дата добавления: 2015-07-10