Метод математической индукции

Утверждение, зависящееотнатурального числа , справедливо для любого , если выполнены два условия:

1) утверждение верно для ;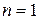

2) из справедливости утверждения для 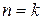, где 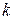- любое натуральное

число, вытекает справедливость утверждения и для следующего натурального числа .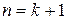

Замечание 1.1. В некоторых случаях утверждение является истинным для , тогда в этом случае пункт 1) проверяют для , а пункт 2) доказывают при . Аналогично, если утверждение выполняется лишь для , тогда пункт 1) проверяют для 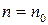, а пункт 2) доказывают при .

Пример 1.11. Доказать, что

.

(1.3)

Решение. 1)Проверим справедливость этого утверждения для 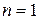, то есть справедливость равенства . Очевидно, .

2) Предположим, что равенство (1.3) выполняется при 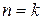, то есть справедливо равенство:

.

(1.4)

Докажем, что тогда проверяемое равенство (1.3) верно и при 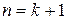, то есть докажем равенство

.

(1.5)

Подчеркнем, что равенство (1.5) интересует нас не само по себе, а интересует вопрос: вытекает ли оно из равенства (1.4).

Рассмотрим левую часть равенства (1.5) и воспользуемся в процессе преобразований равенством (1.4):

.

Таким образом, из равенства (1.4) вытекает равенство (1.5). Оба условия принципа математической индукции выполнены, следовательно, равенство (1.3) справедливо для любого натурального числа .

Пример 1.12. Доказать, что при

Решение. 1)При имеем: 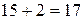- делится на 17.

2) Предположим, что утверждение выполняется при 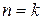, то есть , (, где 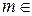), и докажем, что оно верно и при 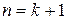, а именно

.

Действительно,

.

Оба условия принципа математической индукции выполняются, следовательно, выдвинутое утверждение доказано.

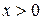Пример 1.13. Доказать, что для и справедливо неравенство

(его называют неравенством Бернулли в честь швейцарского математика Якоба Бернулли (1654-1705)).

Решение. 1)При получим верное неравенство:

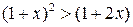(так как )

2) Предположим, что неравенство Бернулли верно для ():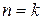

.

(1.6)

Докажем, что неравенство Бернулли верно и для 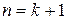, то есть докажем, что

.

Умножим обе части неравенства (1.6) на одно и тоже положительное число 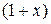, тогда получим:

,

что и требовалось доказать. Следовательно, по принципу математической индукции неравенство Бернулли справедливо для любого .

Дата добавления: 2015-07-10